T-I-3draft

Radon transform and X-ray tomography

The goal of this homework is to introduce the Radon transform of a two-dimensional function. We will show that this transform is invertible and the inverse involves the Fourier transform in two dimensions. From a practical point of view, the Radon transform is the basis of X-ray tomography (as well as X-ray scanning), applied in the medical context in order to obtain cross-section images of different organs. The second part of the homework consists of a documentation work to be conducted in pairs: each pair of students should prepare a blackboard presentation of approximately five minutes on this part.

Radon transform

Preliminaries: parametrisation of a line in the plane

Figure 1: Parametrisation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (t,\Phi)} of a line in the plane.)

Q1: In a two-dimensional space, how many parameters are needed in order to define a line? Provide some examples of equations that define a unique line in the plane.

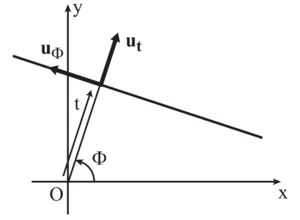
Q2: In the context of Radon transform, we choose to define a line via the parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (t,\Phi)\in \mathbb{R}\times [0;2\pi[} , displayed in Figure 1. Each angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} is associated to a unique unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u_t}} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u_t} = \cos(\Phi) \mathbf{u_x}+ \sin(\Phi)\mathbf{u_y}.}

Show that for each given line there exist two possible pairs of values Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (t,\Phi)} .

Q3: We choose to orient the line positively along the unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u_{\Phi}}} , defined by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u_{\Phi}} = -\sin(\Phi)\mathbf{u_x} + \cos(\Phi)\mathbf{u_y}.}

Show that for each pair <math>(t,\Phi)</math/> there exists a unique oriented line.