T-I-3draft

Radon transform and X-ray tomography

The goal of this homework is to introduce the Radon transform of a two-dimensional function. We will show that this transform is invertible and the inverse involves the Fourier transform in two dimensions. From a practical point of view, the Radon transform is the basis of X-ray tomography (as well as X-ray scanning), applied in the medical context in order to obtain cross-section images of different organs. The second part of the homework consists of a documentation work to be conducted in pairs: each pair of students should prepare a blackboard presentation of approximately five minutes on this part.

Radon transform

Preliminaries: parametrisation of a line in the plane

Figure 1: Parametrisation $(t,\Phi )$ of a line in the plane.)

Q1: In a two-dimensional space, how many parameters are needed in order to define a line? Provide some examples of equations that define a unique line in the plane.

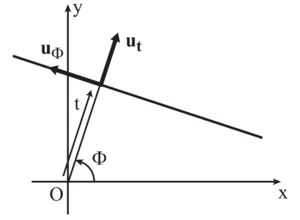
Q2: In the context of Radon transform, we choose to define a line via the parameters $t$ and $\Phi$, where $(t,\Phi )\in \mathbb {R} \times [0;2\pi [$, displayed in Figure 1. Each angle $\Phi$ is associated to a unique unit vector $\mathbf {u_{t}}$:

$\mathbf {u_{t}} =\cos(\Phi )\mathbf {u_{x}} +\sin(\Phi )\mathbf {u_{y}} .$

Show that for each given line there exist two possible pairs of values $(t,\Phi )$.

Q3: We choose to orient the line positively along the unit vector $\mathbf {u_{\Phi }}$, defined by:

$\mathbf {u_{\Phi }} =-\sin(\Phi )\mathbf {u_{x}} +\cos(\Phi )\mathbf {u_{y}} .$

Show that for each pair $(t,\Phi )$ there exists a unique oriented line.

Q4: A natural pair of coordinates, associated to the family of lines obtained from a given $\Phi$, is the pair $(t,s)\in \mathbb {R} ^{2}$ of coordinates of a point in the basis $(\mathbf {u_{t}} ,\mathbf {u_{\Phi }} )$ related to the line that passes through that point. Provide the expression for $(x,y)$ as a function of $(t,s)$, as well as the expression for $(t,s)$ as a function of $(x,y)$. Deduce the relation between the surface elements ${\textrm {d}}x\,{\textrm {d}}y$ and ${\textrm {d}}s\,{\textrm {d}}t$.

Definition of Radon transform

Definition: The Radon transform of a function $f:\mathbb {R} ^{2}\rightarrow \mathbb {R}$ is the function ${\hat {f}}:\mathbb {R} ^{2}\rightarrow \mathbb {R}$ defined by the following expression

${\hat {f}}(t,\mathbf {u_{t}} )=\int _{-\infty }^{+\infty }f(t\mathbf {u_{t}} +s\mathbf {u_{\Phi }} )\,\mathrm {d} s.$

Use of the $\delta -$distribution: The definition of Radon transform can be elegantly written by means of the Dirac-delta distribution. This formulation provides the advantage of generalising the definition of Radon transform to arbitrary dimension.

Q5: Using the relation

$f(t\mathbf {u_{t}} +s\mathbf {u_{\Phi }} )=\int _{-\infty }^{+\infty }f(t'\mathbf {u_{t'}} +s\mathbf {u_{\Phi }} )\delta (t'-t)\mathrm {d} t',$

propose a definition of Radon transform in the form of a surface integral.

Q6: Propose a definition of the Radon transform of a function $f:\mathbb {R} ^{n}\rightarrow \mathbb {R}$ ($n\geq 2$). Give a geometrical interpretation of the Radon transform in dimension $n=3$.

From now on, we will always consider the Radon transform in the two-dimensional case $n=2$.