T-II-2new: Difference between revisions
| Line 92: | Line 92: | ||
<center><math> \rho(\vec r,t)=\rho+\delta \rho(\vec r,t)=\rho\left( 1+\sigma(\vec r,t)\right)</math> </center> | <center><math> \rho(\vec r,t)=\rho+\delta \rho(\vec r,t)=\rho\left( 1+\sigma(\vec r,t)\right)</math> </center> | ||
The scalar field <math> \sigma(\vec r,t)</math> represents the relative fluctuation of the density. | The scalar field <math> \sigma(\vec r,t)</math> represents the relative fluctuation of the density. | ||
* Using the continuity equation of | * Using the continuity equation of a fluid: | ||
<center> <math>\partial_t \rho(r,t)=-\rho \vec{\nabla} \cdot \partial_t \vec{u}(\vec{r},t)</math> </center> | <center> <math>\partial_t \rho(r,t)=-\rho \vec{\nabla} \cdot \partial_t \vec{u}(\vec{r},t)</math> </center> | ||
show that | show that | ||
<center> <math> \sigma(\vec{r},t)= - \vec{\nabla} \cdot \vec{u}(\vec{r},t) </math> </center> | <center> <math> \sigma(\vec{r},t)= - \vec{\nabla} \cdot \vec{u}(\vec{r},t) </math> </center> | ||
and that the previous equation corresponds to the D'Alembert Equation for the scalar field <math> \sigma(\vec r,t) </math> | and that the previous equation corresponds to the D'Alembert Equation for the scalar field <math> \sigma(\vec r,t) </math>. | ||
Conclude that the elastic field in fluids is scalar. | |||
| Line 105: | Line 104: | ||
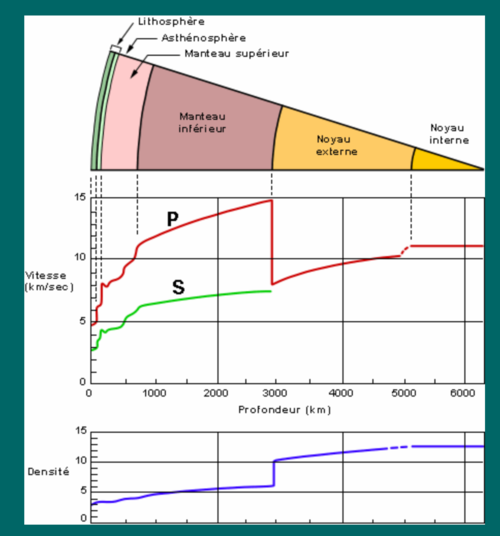
[[File:earthsturcture.png|500px|thumb|left| Men landed on the Moon 50 years ago, but today a Journey to the Center of the Earth remains science fiction. Many scientific operation funded drilling holes through the ocean floor, but they all failed to reach the first discontinuity: ''the external mantel''. However elastic wave can travel their journey probes the internal structure of our Planet. For example we know that there is a fluid external core because secondary waves cannot go deeper than 3000 Km. | |||
]] | |||
==Sound speed in perfect gas== | |||
Generally speaking, a sound wave in an ideal gas oscillates sufficiently rapidly that heat is unable to flow fast enough to smooth out any temperature perturbations generated by the wave. Under these circumstances, the gas obeys the adiabatic gas law, | Generally speaking, a sound wave in an ideal gas oscillates sufficiently rapidly that heat is unable to flow fast enough to smooth out any temperature perturbations generated by the wave. Under these circumstances, the gas obeys the adiabatic gas law, | ||
<center><math>P V^\gamma= </math> constant</center> | <center><math>P V^\gamma= </math> constant</center> | ||
where <math>\gamma</math> the ratio of specific heats (i.e., the ratio of the gas's specific heat at constant pressure to its specific heat at constant volume). This ratio is approximately <math>1.4 </math> for ordinary air. | where <math>\gamma</math> the ratio of specific heats (i.e., the ratio of the gas's specific heat at constant pressure to its specific heat at constant volume). This ratio is approximately <math>1.4 </math> for ordinary air. | ||
* Show that the Lagrangian density writes | * Show that the Lagrangian density writes | ||
<center><math> \mathcal{L} (\vec{r},t) = \frac{\rho_0}{2} \dot{\vec{u}}^2 + P_0 \vec{\nabla} \cdot \vec{u} -\frac{\gamma}{2} P_0 (\vec{\nabla} \cdot \vec{u})^2 </math></center> | <center><math> \mathcal{L} (\vec{r},t) = \frac{\rho_0}{2} \dot{\vec{u}}^2 + P_0 \vec{\nabla} \cdot \vec{u} -\frac{\gamma}{2} P_0 (\vec{\nabla} \cdot \vec{u})^2 </math></center> | ||
* Show that the associated equation of motion | * Show that the associated equation of motion | ||
<center><math> \rho_0 \frac{\partial^2 \vec{u}}{\partial t^2} -\gamma P_0 \vec{\nabla} \vec{\nabla} \cdot \vec{u}=0 </math></center> | <center><math> \rho_0 \frac{\partial^2 \vec{u}}{\partial t^2} -\gamma P_0 \vec{\nabla} \vec{\nabla} \cdot \vec{u}=0 </math></center> | ||
Revision as of 22:20, 2 October 2019
Variational methods: Sound waves in solid and fluid materials
Elasticity in solids
Under the action of external forces a solid body moves. But it can also be deformed, i.e. it can change volume and shape. The first succesful attempt to describe this phenomenon is provided by the theory of elasticity. The theory is based on the assumptions that (1) the solid body can modeled as a continuum medium and (2) the energetic cost of the deformation is kept at the lowest order in perturbation. The fundamental equations of elasticity have been established by Cauchy and Poisson in the twenties of the 19th century, well before the discovery of the atomic structure of matter. An important experimental observation is that a sudden deformation induces small oscillations propagating in the material. Here we derive their equations of motion which describe how the sound propagate in solids.
The strain tensor
We consider a perfectly isotropic continuum medium and assume that at time a body is at rest and no external forces are applied. Each point of the body can be identified with its postion in the space:
Then a sudden deformation is applied and the point located in moves to a new location at time . The displacement, , differs from point to point of the body and is then a function of the original position . The displacement vectorial field
encodes then all informations about the deformation of the body. However large displacements does not always correspond to large deformation as the body can move rigidly without deformation. To quantify how much a body is deformed we consider two points at an infinitesimal distance .
- Assuming small deformations, show that the distance after the deformation can be written as:
The tensor is called strain tensor, is symmetric and defined as
- Consider now a volume element and show that at the first order in perturbation one has
This means that the trace of the strain tensor identifies with the relative change in volume of the body. In general all deformation can be represented as the sum of a uniform compression (change in volume without change of shape) and a shear (change of shape without change of volume):
The first term is a shear as its trace is zero. The second term is a compression.
Energy considerations
The total energy of the body is given by the sum of the elastic and kinetic energy (the gravity is neglected). A body at rest, in abscence of external force and at thermal equilibrium does not display any deformation, this means that when the strain tensor is zero for all points, the potential energy displays a minimum. As a consequence for small deformations the first terms of the expansion of the potential energy must be quadratic in the strain tensor (elastic approximation). The more general quadratic form can be written as , where the tensor contains all the elastic moduli. For an isotropic material the energy cost should be frame independent and we can write a simpler quadratic form that we will discuss in class:
The first term accounts for the cost of the change in volume, the second for the change of shape. The positive constants are respectively the bulk and the shear modulus and have dimensions of a pressure. These two constants are material dependent and fully describe its elastic properties.
The kinetic energy can then be written as
where the mass density and we used the fact that the mass contained in an infinitesimal volume around the point located in is .
The action for a simplified model
We have now all ingredients to write the equation of motion of the displacement fields . To simplify the calculation we first discuss the case where displacements are function only of the coordinate:
this means that two point with the same will have exactly the same displacement.
- Replace by and write the elastic energy in term of
The action associated to this energy is
where is the Lagrangian denisty
- Write explicitly .
- Using the variational methods write the 3 equations of motion for .
- Show that u_x(\vec r, t)Compute the longitudinal mode velocity and the transverse mode velocity.
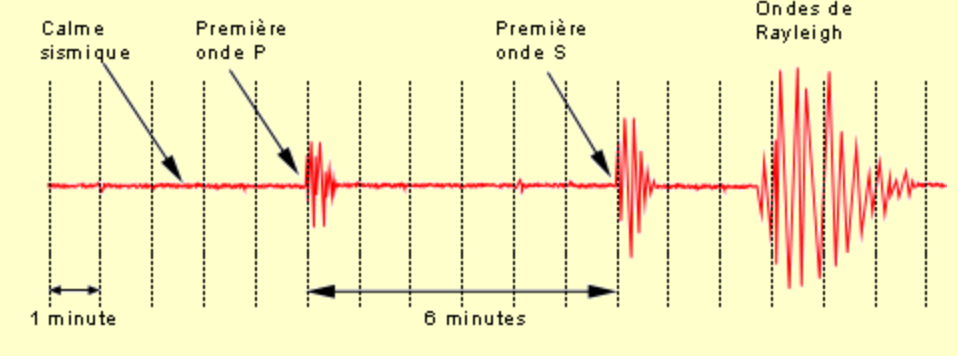
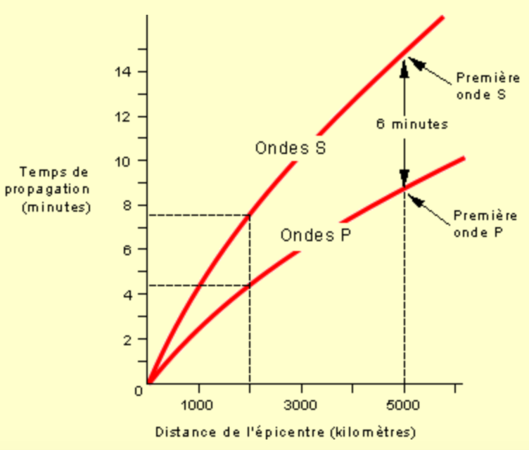
Seismic waves recorded by a seismograph after an earthquake. Longitudinal waves are the quickest and for this reason called primary (P-waves), then arrive the transverse waves, for this reason called secondary (S-waves). Finally it's the turn of Rayleigh waves which are also solution of the D'Alembert equation but propagate only on the Earth surface. They are slower and less damped then bulk waves.
Elasticity in fluids
A fluid does not oppose a change in its shape with any internal resistance. On the other hand a compression has a finite energy cost that we can write
- Show that the Lagrangian density writes
- Show that the associated equation of motion
During the oscillations the mass density can have small fluctuations
The scalar field represents the relative fluctuation of the density.
- Using the continuity equation of a fluid:
show that
and that the previous equation corresponds to the D'Alembert Equation for the scalar field . Conclude that the elastic field in fluids is scalar.
Sound speed in perfect gas
Generally speaking, a sound wave in an ideal gas oscillates sufficiently rapidly that heat is unable to flow fast enough to smooth out any temperature perturbations generated by the wave. Under these circumstances, the gas obeys the adiabatic gas law,
where the ratio of specific heats (i.e., the ratio of the gas's specific heat at constant pressure to its specific heat at constant volume). This ratio is approximately for ordinary air.
- Show that the Lagrangian density writes
- Show that the associated equation of motion


















![{\displaystyle E_{\text{el}}=\int d{\vec {r}}\left[{\frac {K}{2}}\sum _{i}\epsilon _{ii}^{2}+\mu \sum _{ik}\left(\epsilon _{ik}-{\frac {1}{3}}\delta _{ik}{\text{Tr}}(\epsilon )\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/859c4586807fd9d94a8968cbf6fa9fd192790ebe)













![{\displaystyle W={\frac {K}{2}}\int d{\vec {r}}\left[\sum _{i}\epsilon _{ii}^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951c189ae916a72491951ec4d5054e5284fa8cea)










