When confronted with the enormous diversity of material properties, it is absolutely fantastic to believe that such diversity arises from the relatively small group of fundamental elements which constitute the periodic table. Indeed, here on earth we have appreciable quantities of roughly only one hundred different elements. So is it really true that this small group of fundamental building blocks accounts for every single thing we have ever seen, heard, tasted, smelt, and felt?
Science is slowly revealing that in fact it is less the individual atom, and more the interactions among atoms which unlock the door to this diversity. By understanding « what form are these interactions » and « what are their consequences » at the level of just two individual, isolated atoms we make our first step toward understanding material properties. And this can be done with our feet remaining firmly planted in the most fundamental theory at our disposal: Quantum physics.
Each element on the periodic table has its own unique shape. This is determined by the way its electrons are configured. Only elements with either half filled or completely filled electronic sub-shells turn out to be spherical, the rest are aspherical. The rare-earth element dysprosium lies in the lanthanide chemistry group and presents a very interesting extremum in that it’s electronic configuration makes it extremely highly ellipsoidal. This ellipticity equates to dysprosium having the strongest interatomic dipole-dipole forces among all common stable elements.
New research published in two recent articles lifts the lid on the consequences of these strong dipolar interactions in ultra-cold dysprosium fluids. When two dysprosium atoms collide, they exchange momenta under the constraints of conserved energy and momentum. The post-collision momenta of the two atoms is statistically determined by the quantum wave-function of the two particles. Indeed, this aspect is similar to all atoms. However, in strongly dipolar atoms such as dysprosium, things get a little more interesting. Here, the distribution of outgoing momenta depends strongly on the orientation of the dipoles relative to the axis along which the atoms collide. The details of such collisions need to be accurately understood in order to understand the dynamics of the entire fluid. Theorists at LPTMS were able to understand these collision events based on an analytic solution to the two-body Schroedinger equation. Furthermore, they went on to incorporate this understanding into a Monte-Carlo simulation algorithm. This technique promotes the information of two-body collisions into an ab-initio theory of the entire gas. Remarkable experimental progress by Professor Benjamin Lev and his team at Stanford University are now able to control isolated mesoscopic clouds of ultra cold dysprosium atoms. Comparisons between the theory and the experiment provided, not only remarkable agreement, but an entirely new method of thermometry in dipolar gases, and a new tool to measure scattering length (particularly in the presence of Fano-Feshbach resonances).
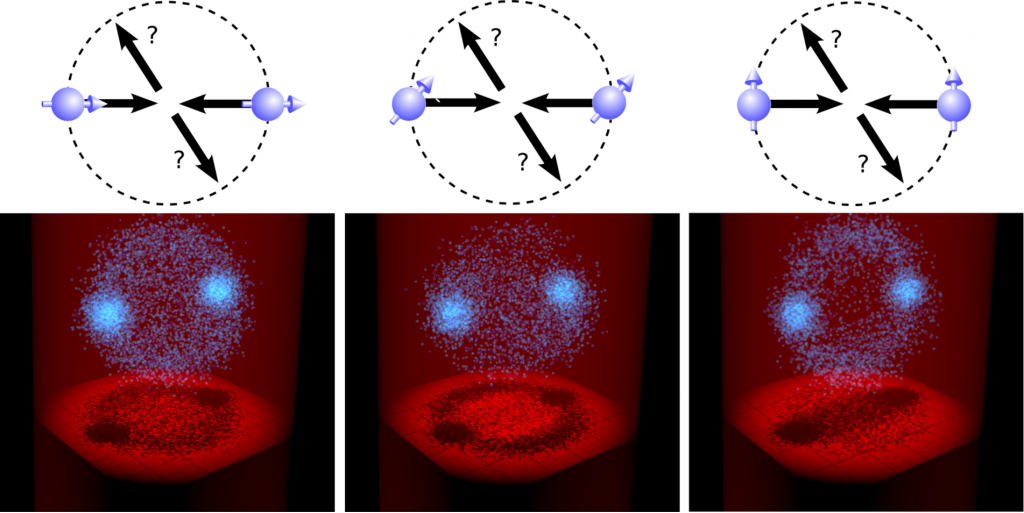
The experiments involve a collision between two oppositely propagating clouds of dysprosium atoms. In the images above (along the bottom row) one can see a snapshot after these clouds have passed through one another. The clearly visible « large blobs » are atoms which never experienced a collision. The other atoms, which appear on the « halo-like » sphere did experience a collision. While conservation of energy and momentum requires all atoms that scatter end up some where on the sphere, the distribution around the sphere is determined by the nature of the interatomic interaction. Moreover, in the case of dipolar interactions, it is furthermore dependent on the dipole alignment direction relative to the collision axis. So, moving along the images from left to right, the dipoles are aligned parallel, forty five degrees, and perpendicular to the collision axis (as shown schematically in the top row). The experiments analyse the atomic clouds by looking at absorption images of their three-dimensional spatial distribution.
References:
N. Q. Burdick, A. G. Sykes, Y. Tang and B. L. Lev, New J. Phys. 18 113004 (2016)