T-2: Difference between revisions
| (145 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<strong>Goal: </strong> deriving the equilibrium phase diagram of the Random Energy Model (REM). Notion such as: freezing transition, entropy crisis, condensation, overlap distribution. <br> | |||
<strong> Techniques: </strong> saddle point approximation, thermodynamics, probability theory. | |||
<br> | |||
=== | == Problems== | ||
In the | === Problem 2: the REM: freezing transition, condensation & glassiness === | ||
In this Problem we compute the equilibrium phase diagram of the model, and in particular the quenched free energy density <math>f(\beta):=f_\infty(\beta) </math> which controls the scaling of the typical value of the partition function, <math>Z_N(\beta) \sim e^{-N \beta \, f(\beta) +o(N) } </math>. We show that the free energy equals to | |||
<center><math> | |||
f(\beta) = | |||
\begin{cases} | |||
&- \left( T \log 2 + \frac{1}{2 T}\right) \quad \text{if} \quad T \geq T_f\\ | |||
& - \sqrt{2 \,\log 2} \quad \text{if} \quad T <T_f | |||
\end{cases} \quad \quad T_f= \frac{1}{ \sqrt{2 \, \log 2}}. | |||
</math></center> | |||
At <math> T_f </math> a transition occurs, often called freezing transition: in the whole low-temperature phase, the free-energy is “frozen” at the value that it has at the critical temperature <math>T= T_f </math>. <br> | |||
We also characterize the overlap distribution of the model: the overlap between two configurations <math> \vec{\sigma}^\alpha, \vec{\sigma}^\beta </math> is | |||
<math>q_{\alpha \, \beta}= N^{-1} \sum_{i=1}^N \sigma_i^\alpha \, \sigma_i^\beta</math>, and its distribution is | |||
<center> | <center> | ||
<math> | <math> | ||
P_{N, \beta}(q)= \sum_{\alpha, \beta} \frac{e^{-\beta E(\vec{\sigma}^\alpha)}}{Z_N}\frac{e^{-\beta E(\vec{\sigma}^\beta)}}{Z_N}\delta(q-q_{\alpha \beta}). | |||
</math> | |||
</center> | |||
</math></center> | |||
<ol> | <ol> | ||
<li> <em> | <li><em> The freezing transition.</em> | ||
The partition function the REM reads | |||
<math> | |||
Z_N(\beta) = \sum_{\alpha=1}^{2^N} e^{-\beta E_\alpha}= \int dE \, \mathcal{N}_N(E) e^{-\beta E}. | |||
</math> | |||
Using the behaviour of the typical value of <math> \mathcal{N}_N </math> determined in Problem 1, derive the free energy of the model (hint: perform a saddle point calculation). What is the order of this thermodynamic transition? | |||
</ | |||
</ol> | </ol> | ||
</li> | </li> | ||
<br> | <br> | ||
<ol start="2"> | <ol start="2"> | ||
<li><em> | <li><em> Fluctuations, and back to average vs typical.</em> Similarly to what we did for the entropy, one can define an annealed free energy <math> f_{\text{a}}(\beta) </math> from <math> \overline{Z_N(\beta)}=e^{- N \beta f_{\text{a}}(\beta) + o(N)} </math>: show that in the whole low-temperature phase this is smaller than the quenched free energy obtained above. Putting all the results together, justify why the average of the partition function in the low-T phase is "dominated by rare events". | ||
</ol></li> | |||
</ | |||
</ | |||
<br> | <br> | ||
<ol start="3"> | <ol start="3"> | ||
<li><em> | <li> <em> Entropy crisis.</em> What happens to the entropy of the model when the critical temperature is reached, and in the low temperature phase? What does this imply for the partition function <math> Z_N</math>?</li> | ||
</li> | |||
</ol> | </ol> | ||
<br> | <br> | ||
= | <ol start="4"><li><em> Overlap distribution and glassiness.</em> | ||
Justify why in the REM the overlap when <math> N \to \infty</math> typically can take only values zero and one, leading to | |||
<center> | <center> | ||
<math> | <math> | ||
P_\beta(q)= \lim_{N \to \infty} \overline{P_{N, \beta}(q)}= \overline{I_2} \, \delta(q-1)+ (1-\overline{I_2}) \, \delta(q), \quad \quad I_2= \lim_{N \to \infty} \frac{\sum_\alpha z_\alpha^2}{\left(\sum_\alpha z_\alpha\right)^2}, \quad \quad z_\alpha=e^{-\beta E_\alpha} | |||
q | |||
\ | |||
</math> | </math> | ||
</center> | </center> | ||
Why <math> I_2 </math> can be interpreted as a probability? Show that | |||
<center> | <center> | ||
<math> | <math> | ||
\overline{I_2} | |||
\ | =\begin{cases} | ||
0 \quad &\text{if} \quad T>T_f\\ | |||
1-\frac{T}{T_f} \quad &\text{if} \quad T \leq T_f | |||
\end{cases} | |||
\quad | |||
\ | |||
\ | |||
\quad | |||
\text{ | |||
\quad | |||
\ | |||
</math> | </math> | ||
</center> | </center> | ||
and interpret the result. In particular, why is this consistent with the entropy crisis? <br> | |||
</li> | <em> Hint: </em> For <math> T<T_f </math>, use that <math> \overline{I_2}=\frac{T_f}{T} \frac{d}{d\mu}\log \int_{0}^\infty (1-e^{-u -\mu u^2})u^{-\frac{T}{T_f}-1} du\Big|_{\mu=0}</math></li> </ol> | ||
</ol> | |||
<br> | <br> | ||
== Comments== | |||
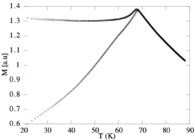
[[File:Suscept-experiment.png|thumb|left|x140px| Experimental measurements of the magnetic Field Cooled (top) and Zero-Field Cooled (bottom) susceptibility in a CuMn spin glass. Figure taken from C. Djurberg, K. Jonason, P. Nordblad, https://arxiv.org/abs/cond-mat/9810314]] | |||
</ | <ol> | ||
<li><em> Glassiness.</em> The low-T phase of the REM is a frozen phase, characterized by the fact that the free energy is temperature independent, and that the typical value of the partition function is very different from the average value. In fact, the low-T phase is also <em> a glass phase </em> with <math> q_{EA}=1</math>. This is also a phase where a peculiar symmetry, the so called replica symmetry, is broken. We go back to this concepts in the next sets of problems. | |||
<br> | |||
<br> | |||
<li><em> The physics: susceptibility and experiments.</em> The magnetic susceptibility of the REM can be computed adding a field to the energy function: <math> E(\vec{\sigma}^\alpha) \to E_\alpha + H \sum_i \sigma^\alpha_i</math>. Redoing the thermodynamics calculation in presence of the field (do its!!) one can show that in the REM | |||
<center><math> | |||
\chi(\beta) = \frac{\partial m(\beta, H) }{\partial H}\Big|_{H=0}= | |||
\begin{cases} | |||
&\frac{\partial \tanh(\beta H) }{\partial H}\Big|_{H=0}= \beta \quad \text{if} \quad T \geq T_f\\ | |||
& \frac{\partial \tanh(\beta_f H) }{\partial H}\Big|_{H=0}= \beta_f \quad \text{if} \quad T <T_f | |||
\end{cases}. | |||
</math></center> | |||
where <math>m(\beta, H)</math> is the equilibrium magnetization. Therefore, the susceptibility does not diverge at the transition, as it happens in standard ferromagnets, but becomes flat (recall that what diverges at the spin-glass transition are non-linear susceptibilities, as discussed in Lecture 1 by Alberto). A similar behavior is found in measurements of the Field-Cooled susceptibility in spin glass systems, and it is captured by the Parisi's solution of the SK model with replicas, which therefore captures the physics probed in experiments. | |||
</li> | </li> | ||
</ol> | </ol> | ||
== Check out: key concepts == | |||
Freezing transition, entropy crisis, condensation, overlap distribution. | |||
== To know more == | |||
* Derrida. Random-energy model: limit of a family of disordered models [https://hal.science/hal-03285940v1/document] | |||
* Derrida. Random-energy model: An exactly solvable model of disordered systems [http://www.lps.ens.fr/~derrida/PAPIERS/1981/prb81.pdf] | |||
Latest revision as of 18:42, 9 February 2025
Goal: deriving the equilibrium phase diagram of the Random Energy Model (REM). Notion such as: freezing transition, entropy crisis, condensation, overlap distribution.
Techniques: saddle point approximation, thermodynamics, probability theory.
Problems
Problem 2: the REM: freezing transition, condensation & glassiness
In this Problem we compute the equilibrium phase diagram of the model, and in particular the quenched free energy density which controls the scaling of the typical value of the partition function, . We show that the free energy equals to
At a transition occurs, often called freezing transition: in the whole low-temperature phase, the free-energy is “frozen” at the value that it has at the critical temperature .
We also characterize the overlap distribution of the model: the overlap between two configurations is
, and its distribution is
- The freezing transition. The partition function the REM reads Using the behaviour of the typical value of determined in Problem 1, derive the free energy of the model (hint: perform a saddle point calculation). What is the order of this thermodynamic transition?
- Fluctuations, and back to average vs typical. Similarly to what we did for the entropy, one can define an annealed free energy from : show that in the whole low-temperature phase this is smaller than the quenched free energy obtained above. Putting all the results together, justify why the average of the partition function in the low-T phase is "dominated by rare events".
- Entropy crisis. What happens to the entropy of the model when the critical temperature is reached, and in the low temperature phase? What does this imply for the partition function ?
- Overlap distribution and glassiness.
Justify why in the REM the overlap when typically can take only values zero and one, leading to
Why can be interpreted as a probability? Show that
and interpret the result. In particular, why is this consistent with the entropy crisis?
Hint: For , use that
Comments
- Glassiness. The low-T phase of the REM is a frozen phase, characterized by the fact that the free energy is temperature independent, and that the typical value of the partition function is very different from the average value. In fact, the low-T phase is also a glass phase with . This is also a phase where a peculiar symmetry, the so called replica symmetry, is broken. We go back to this concepts in the next sets of problems.
- The physics: susceptibility and experiments. The magnetic susceptibility of the REM can be computed adding a field to the energy function: . Redoing the thermodynamics calculation in presence of the field (do its!!) one can show that in the REM
where is the equilibrium magnetization. Therefore, the susceptibility does not diverge at the transition, as it happens in standard ferromagnets, but becomes flat (recall that what diverges at the spin-glass transition are non-linear susceptibilities, as discussed in Lecture 1 by Alberto). A similar behavior is found in measurements of the Field-Cooled susceptibility in spin glass systems, and it is captured by the Parisi's solution of the SK model with replicas, which therefore captures the physics probed in experiments.
Check out: key concepts
Freezing transition, entropy crisis, condensation, overlap distribution.






















