T-4

Goal: Understand some physical properties of mean-field spin glasses in the low-T phase: the structure of the free-energy landscape, the response of the system to applied magnetic fields.

Key concepts: full-RSB, magnetic susceptibility, linear response.

Replica solutions: a classification

File:SketchRSB.png

Decomposition of configuration space into states

• 1-RSB. We have seen an example of mean-field model, the spherical Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} -spin, in which the low-T phase is glassy, described by a 1-RSB ansatz of the overlap matrix. The equilibrium in the glassy phase is described by three quantities: the typical overlap Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_1^{SP} } between configurations belonging to the same pure state, the typical overlap Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_0^{SP} } between configurations belonging to different pure states, and the probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-m^{SP}) } that two configurations extracted at equilibrium belong to the same state. It can be shown that the low-T, frozen phase of the REM is also described by this 1-RSB ansatz with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_0^{SP}=0, q_1^{SP}=1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m^{SP}=T/T_c } .


• full-RSB. The Sherrington-Kirkpatrick model introduced in Lecture 1 also has a low-T phase that is glassy. However, the structure of the free-energy landscape is more complicated and encoded in a complicated pattern of the mutual overlaps between equilibrium states. To understand it, let us consider a 2-RSB ansatz for the overlap matrix:

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=\begin{pmatrix} 1 & q_2 &q_1& q_1 & q_0 \cdots& q_0\\ q_2 & 1 &q_1& q_1 & q_0 \cdots& q_0\\ q_1 & q_1 &1& q_2 & q_0 \cdots& q_0\\ q_1 & q_1 &q_2& 1 & q_0 \cdots& q_0\\ \cdots\\ \cdots\\ \cdots\\ q_0 & q_0 \cdots& q_2&1 & q_1 &q_1\\ q_0 & q_0 \cdots& q_1&q_1 & 1 &q_2\\ q_0 & q_0 \cdots& q_1&q_1 & q_2 &1\\ \end{pmatrix} }

  which assumes that replicas are split into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1} blocks, and that inside each block they are further split into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2<m_1} blocks (in the example above,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1=4, m_2=2} ). This is also not the correct structure for the SK model. The correct one obtained iterating this procedure an infinite number of times, as understood by Parisi [2]. Iterating K times, one ends up with a series of overlaps Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_K > q_{K-1} > \cdots >q_0} . The underlying picture of the free-energy landscape is as follows: equilibrium states have self-overlap Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_K = q_{EA}} . They are arranged in clusters such that states inside a cluster have overlap Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_{K-1}} , but such clusters are arranged in other clusters at a higher level, at mutual overlap Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_{K-2}} and so on. The Parisi solution of the Sherrington Kirkpatrick model is obtained taking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K \to \infty} . In this limit, the overlap distribution becomes a continuous distribution.


• Properties.

Problems

Problem 4.1: magnetic susceptibilities and linear response

In an Ising system, the thermodynamic magnetic susceptibility is defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{eq}= \frac{d m( h)}{dh}\Big|_{h=0} }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m(h)=\lim_{N \to \infty} m_N(h)} is the magnetization at a given inverse temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} and external field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_N(h)} its finite-size counterpart. The function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{eq}} measures the response to changes of the magnetic field.

1. Ferromagnetism. Using the self-consistent equation for the magnetization in the mean-field Ising model, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m= \text{tanh}[\beta(h+m)]} , show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{eq}} diverges exactly at the transition temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta=\beta_c=1} .

2. Spin glass. By the Fluctuation-Dissipation Theorem (FDT), we know that the response and correlations at equilibrium are related by

   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_N= \frac{d m_N( h)}{dh} \Big|_{h=0}= \frac{\beta}{N}\sum_{ij} \overline{\langle \sigma_i \sigma_j \rangle_{c}} =\frac{\beta}{N}\sum_{ij} \overline{\langle \sigma_i \sigma_j \rangle- \langle \sigma_i \rangle \langle \sigma_j \rangle }. }

   In a spin glass, by symmetry with respect to sign flips of the couplings it holds Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\langle \sigma_i \sigma_j \rangle_c}= 0} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \neq j } . Show that one can write

   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{eq}=\lim_{N \to \infty}\chi_N = \beta \left( 1-\int dq\, \overline{P(q)}\, q \right) \, \quad \quad \quad \overline{P(q)}= \overline{\sum_{\alpha, \beta} \omega_\alpha \omega_\beta \delta(q-q_{\alpha \beta})}}

   and thus that this quantity does not diverge at the transition to the spin-glass phase.

3. “Failure” of linear response. The quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{eq} } is however not what one measures in linear response in spin glasses! Indeed, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{eq} } is the response that one would measure if the system is prepared at equilibrium, then a small magnetic field is applied and the system is given enough time to reach the new equilibrium state. ^[1] In linear response, one would measure however the response Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{LR} } of the system which is confined to a given pure state: in analogy with the above, what would you expect to be its expression in terms of the overlaps? Could you explain intuitively why Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{LR}< \chi_{eq}} ?

The ZFC (lower curve) and FC (upper curve) susceptibility. Experimental results taken from [1]

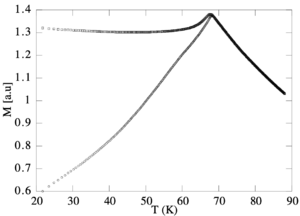
4. Experiments. The plot on the left shows experimental measurements of the magnetic susceptibility in a spin-glass. The two curves correspond to two different protocols: (i) ZFC (zero-field cooled) protocol: cool the system at low T, add a very small magnetic field when the system is already at the final low temperature; (ii) FC (field-cooled): cooling the system in presence of a small magnetic field and comparing the observed magnetization with the one measured without this small magnetic field. In the second protocol, the system has the ability to choose the state that is most appropriate in presence of the applied field. Which of the the two susceptibilities defined above describe these two experimental protocols?

Comment: the magnetic susceptibility does not diverge at the spin-glass critical temperature. One can identify a more complicated object, the spin-glass susceptibility , that does diverge at the transition. At variance with the magnetic susceptibility, that is related to a 2-point function (the correlation, which involves two spins), the spin-glass susceptibility is associated to a 4-point function. This is consistent with the fact that the order parameter of the spin-glass phase, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_{EA} } , is itself a 2-point function, while the magnetization that is a 1-point function. -->