L-7

Goal : This is the first lecture about the localization. Localization is a wave phenomenon induced by disorder.

Free particles and ballistic behaviour

The Schrodinger equation govern the evolution of the quantum state of a particle in 1D:

$i\hbar \,\partial _{t}\psi (x,t)=H\psi (x,t),\quad H=-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}+V(x)$

Here $H$ is the Hamiltonian. For a free particle the potential is absent, $V(x)=0$.

One first look for separable solutions, or eigenstates or stationary solutions. These solutions are stationary because if the particle is in an eigenstate, its physical properties are time independent. For a free particle, the separable solutions have the form

$\psi _{k}(x,t)={\frac {1}{\sqrt {2\pi }}}e^{ikx}e^{-iE_{k}t/\hbar },\quad {\text{with}}\;E_{k}={\frac {\hbar ^{2}k^{2}}{2m}}$

Here $k$ is a real number, hence the spectrum is continuum. These solutions are delocalized on the entire real axis and they cannot be normalized.

The physical states of the particle can be decomposed on the eigenstates of the Hamiltonian. Indeed, For the superposition principle, any linear combination of separable solution is also a solution of the Schrodinger equation. However this superposed solution are not separable and the particle's properties will evolve in time. Hence, we can costruct a localized wave packet, with the correct normalization:

$\psi (x,t)=\int _{-\infty }^{\infty }dkc(k)\psi _{k}(x,t),\quad {\text{with}}\;\int _{-\infty }^{\infty }dk|c(k)|^{2}=1$

Evolution of the Gaussian packet

• Initial state . At time $t=0$, the wave packet and its probability density function are

$\psi (x,t=0)={\frac {e^{-x^{2}/(4a^{2})}}{(2\pi a^{2})^{1/4}}},\quad |\psi (x,t=0)|^{2}={\frac {e^{-x^{2}/(2a^{2}))}}{\sqrt {2\pi a^{2}}}}$

Show that the coefficent $c(k)$ are

$c_{k}=\left({\frac {2a^{2}}{\pi }}\right)^{1/4}e^{-a^{2}k^{2}}$

• Time evolution . We define the spreading speed $v_{s}=\hbar /(2ma^{2})$. Show that the time evolution of the Gaussian wave packet has the form:

$\psi (x,t)={\frac {e^{-x^{2}/(4a^{2}(1+iv_{s}t))}}{[2\pi a^{2}(1+iv_{s}t)]^{1/4}}}$

• Ballistic Spreading. Show that the Probability density function of the position is

$|\psi (x,t)|^{2}={\frac {e^{-x^{2}/(2a^{2}(1+v_{s}^{2}t^{2}))}}{[2\pi a^{2}(1+v_{s}^{2}t^{2})]^{1/2}}}$

Hence, the particle spreads on a distance

${\sqrt {\langle x^{2}\rangle }}\equiv \left(\int _{-\infty }^{\infty }dxx^{2}|\psi (x,t)|^{2}\right)^{1/2}=a{\sqrt {1+v_{s}^{2}t^{2}}}$

Localization of the packet: General idea and experiment

BCE condensate confined with an harmonic trap in a 1D disordered geometry. Billy et al, Nature 2008

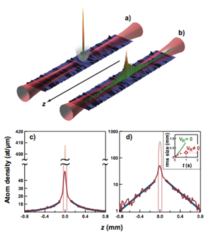
In 1958, P. Anderson proposed that disorder can quench the dynamics of non ineracting particles. This phenomenon, called Anderson localization, is very well observed in numerical simulations. Recenlty, it has been clearly observed in experiments. Here, a Gaussian packet of a BCE is prepared with an harmonic trap. When the trap is removed, particles start to spread, but remain quickly localized in space.

To explain how this is possible we need to solve the eigenstate problem of the hamiltonian with a disorder potential $V(x)$, e.g. a Gaussian white noise. We will study this problem in different dimensions and see that eigenstates can be localized in space.

Semilog plot of the particle concentration. Billy et al, Nature 2008

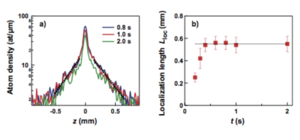
In this case an eigenstate $\psi _{k}(x,t)$ of energy $E_{k}$ is concentrated around some position ${\overline {x}}$. Far from its center, the wave function decays exponentially with a finite localization length: $\xi _{\text{loc}}(E_{k})$ (this length has a mild dependence on $E_{k}$ that we neglect for the moment).

$\psi _{k}(x,t)=\psi _{k}(x)e^{-iE_{k}t/\hbar },\quad {\text{with}}\;\psi _{k}(x)\sim e^{-{\frac {|x-{\overline {x}}|}{\xi _{\text{loc}}(E_{k})}}}$

In the experiment an exponential decay of the Gaussian packet has been clearly shown. How it is related with the exponential decay of the eigenstates? To describe the evolution of the packet, we proceed as before:

• First, decompose the wave packet as a superposition on the new eigenstates. The coefficients $c(k)$ are concentrated only on the eigenstates which are localized around the packet.
• Second, evolve the packet in a given point as the superposition of the time evolved eigenstates in that point.
• It is time for two crucial observations: Eigenstates localized far away from the packet provide an exponetially small contribution it. Viceversa, the eigenstates on which the packet is decomposed provide an exponentially small contribution far away from it.

As a consequence, transport far away from the initial location of the particle is exponentially suppressed.

The conductance and the diffusive behaviour

The main effect of disorder in real material is not localization, but is that transport is diffusive. Indeed, from the time of Drude model, we know that electrons scatter on the impurities with a random velocity. Beyond the mean free path an electron perform a random walk in the material. We will no go into that, but we will assume that if the effect of the disorder is weak, the material is a conductor and obeys Ohm's laws:

• First law:

${\frac {V}{I}}=R,\quad {\text{or}}\quad {\frac {I}{V}}=G$

Here $R$ is the resistence of the sample and $G$ is its conductance.

• Second law

$R=\rho {\frac {L}{S}}\sim \rho L^{2-d},\quad {\text{or}}\quad G=\sigma {\frac {S}{L}}\sim \sigma L^{d-2}$

Here $\rho ,\sigma$ are the resistivity and the conductivity. These are material properties, independent of the geometry of the sample. Let us stress once again that these two phenomenological laws are a macroscpic manifestation of the diffusive motion of the electrons.

Conductance in presence of a localized spectrum

If the effect of the disorder is strong also diffusion is suppressed. The conductance in presence of localization decay exponentially

$G\sim e^{-2L/\xi _{\text{loc}}}$

There are different ways to derive this result here we use the Landauer model.

We present the idea $d=1$ and consider a problem in which disorder is present only in a box of size $(0,L)$.

• Construct the scattering states of energy $E={\frac {\hbar ^{2}k^{2}}{2m}}$. Far from the box the states are plane waves coming from the left:

$\psi _{k,L}(x)={\begin{cases}(e^{ikx}+re^{-ikx})\quad &{\text{for}}\;\;x\to -\infty \\te^{ikx}\quad &{\text{for}}\;\;x\to \infty \end{cases}}$

or coming from the right

$\psi _{k,R}(x)={\begin{cases}(e^{-ikx}+re^{ikx})\quad &{\text{for}}\;\;x\to \infty \\te^{-ikx}\quad &{\text{for}}\;\;x\to -\infty \end{cases}}$

• The current probability of a wave function in 1D writes

$J={\frac {\hbar }{2mi}}\left(\psi ^{*}{\frac {d\psi }{dx}}-\psi {\frac {d\psi ^{*}}{dx}}\right)$

Hence you can derive

$J_{k,L}=-J_{-k,R}={\frac {\hbar k}{m}}|t|^{2}$

• In the Laundauer model we apply a voltage $V$ and meassure the current as the sum of $J_{k,L}$ up to the energy $E_{F}+eV$ and of $J_{k,L}$ up to $E_{F}$. Pay attention to the Jacobian ${\frac {\hbar ^{2}k}{m}}dk=dE$ and get:

$I=e\int _{0}^{E_{F}+eV}{\frac {mdE}{\hbar ^{2}k}}J_{k,L}+e\int _{0}^{E_{F}}{\frac {mdE}{\hbar ^{2}k}}J_{-k,R}\sim {\frac {e^{2}}{\hbar }}|t|^{2}V$

Conclude

$G={\frac {e^{2}}{\hbar }}|t|^{2}$

• If the sample is in the localized phase we can expect

$|t|^{2}=e^{-{\frac {2L}{\xi _{\text{loc}}}}}$

The gang of the four

In a famous PRL (1979) four physicists, Abrahams, Anderson, Licciardello, Ramakrishnan, proposed a scaling theory for localization. It provides a valid argument on the fate of localization at different dimensions. It is based on two well justified assumptions:

• Single parameter scaling (due to Thouless): the RG equation of the dimensionless conductance $g=G\hbar /e^{2}$ is a function of the dimension and of $g$ only:

${\frac {d\ln g}{d\ln L}}=\beta (g)$

The beta function is unknown and the $\ln g$ mean we are interested in the typical behaviour instead of the mean behaviour.

• Asymptotic behaviour: For large conductance we can assume that the material (at these scales) is a conductor, for very small conductance we take instead the insulating behaviour. Hence

$\beta (g)={\begin{cases}d-2\quad &{\text{for}}\;\;g\to \infty \\-{\frac {2L}{\xi _{\text{loc}}}}=\ln g\quad &{\text{for}}\;\;g\to -\infty \end{cases}}$

The simplest scenario is that the beta function is monotonous. Within this picture, we expect a single metal-insulator transition for $d>2$ and a fully localized phase at $d=2$ and below. More complex scenarios, with multiple transitions go against physical intuition.