L-3

Goal: This lecture is dedicated to a classical model in disordered systems: the directed polymer in random media. It has been introduced to model vortices in superconductur or domain wall in magnetic film. We will focus here on the algorithms that identify the ground state or compute the free energy at temperature T, as well as, on the Cole-Hopf transformation that map this model on the KPZ equation.

Polymers, interfaces and manifolds in random media

We consider the following potential energy

$E_{pot}=\int dr{\frac {\sigma }{2}}(\nabla h)^{2}+V(r,h)$

The first term represents the elasticity of the manifold and the second term is the quenched disorder, due to the impurities. In general, the medium is D-dimensional, the internal coordinate of the manifold is d-dimensional and the height filed is N-dimensional. Hence,the following equations always holds:

$D=d+N$

In practice, we will study two cases:

• Directed Polymers ($d=1$), $D=1+N$. Examples are vortices, fronts...
• Elastic interfaces ($N=1$), $D=d+1$. Examples are domain walls...

Today we restrict to polymers. Note that they are directed because their configuration $h(r)$ is uni-valuated.

Directed polymers

Dijkstra Algorithm and transfer matrix

Sketch of the discrete Directed Polymer model. At each time the polymer grows either one step left either one step right. A random energy $V(\tau ,x)$ is associated at each node and the total energy is simply $E[x(\tau )]=\sum _{\tau =0}^{t}V(\tau ,x)$.

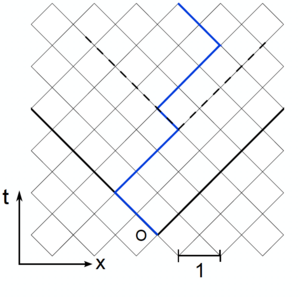
We introduce a lattice model for the directed polymer (see figure). In a companion notebook we provide the implementation of the powerful Dijkstra algorithm that allows to identify the ground state energy $E_{\min }$ :

$E_{\min }=\min _{x(\tau )}E[x(\tau )],\quad E[x_{\min }(\tau )]=E_{\min }$

as well as the ground state configuration $x_{\min }(\tau )$. A self similar behaviour is expected for the energy fluctuations, namely:

$E_{\min }=c_{2}^{\infty }t+t^{\theta }\chi ,\quad x_{\min }(t/2))\sim t^{\zeta }{\tilde {\chi }}$

Let's define two different boundary conditions:

• Droplet: $x(\tau =0)=x(\tau =t)=0$.
• Flat BC: $x(\tau =0)=0$ while the other end $x(\tau =t)$ is free.

Back to the continuum model, a quantuum approach

It is useful to re-write the model using the following change of variable

$h\to x,\quad r\to t$

To fix the idea we can consider polymers of length $t$, starting in $x_{0}$ and ending in $x_{t}$. We sum over all possible polymers to compute the partition function at temperature $T=1$

$Z[x_{t},t;x_{0},0]=\int _{x(0)=x_{0}}^{x(t)=x_{t}}{\cal {D}}x\exp \left[-\int _{0}^{t}d\tau (\partial _{\tau }x)^{2}+V(x,\tau )\right]$

The previous equation gives the path integral expression of the propagator for a quantum particle, in the imaginary time. Note the the potential is a white noise and thus a time dependent potential.

In the spirit of the Feyman Kac formula we write the time-dependent Hamiltonian of the particle

${\hat {H}}=-{\frac {d^{2}}{dx^{2}}}+V(x,\tau )$

Hhe partition function is the solution of the Schrodinger-like equation:

$\partial _{t}Z=-{\hat {H}}Z={\frac {d^{2}Z}{dx^{2}}}-V(x,\tau )Z$

The initial condition is $Z[x_{t},t=0;x_{0},0]=\delta (x-x_{0})$.

DISCUTERE CON SATYA LEGAMI FEYMAN KAC FORMULA / transfer matrix

In this equation the noise is multiplicative and not additive as in the previous lecture. However, all KPZ results can be employed today, thanks to the Cole Hopf transformation.