L-3

Goal: This lecture is dedicated to a classical model in disordered systems: the directed polymer in random media. It has been introduced to model vortices in superconductur or domain wall in magnetic film. We will focus here on the algorithms that identify the ground state or compute the free energy at temperature T, as well as, on the Cole-Hopf transformation that map this model on the KPZ equation.

Polymers, interfaces and manifolds in random media

We consider the following potential energy

$E_{pot}=\int dr{\frac {1}{2}}(\nabla h)^{2}+V(h(r),r)$

The first term represents the elasticity of the manifold and the second term is the quenched disorder, due to the impurities. In general, the medium is D-dimensional, the internal coordinate of the manifold is d-dimensional and the height filed is N-dimensional. Hence,the following equations always holds:

$D=d+N$

In practice, we will study two cases:

• Directed Polymers ($d=1$), $D=1+N$. Examples are vortices, fronts...
• Elastic interfaces ($N=1$), $D=d+1$. Examples are domain walls...

Today we restrict to polymers. Note that they are directed because their configuration $h(r)$ is uni-valuated. It is useful to study the model using the following change of variable

$h\to x,\quad r\to t$

Directed polymers

Dijkstra Algorithm and transfer matrix

Sketch of the discrete Directed Polymer model. At each time the polymer grows either one step left either one step right. A random energy $V(\tau ,x)$ is associated at each node and the total energy is simply $E[x(\tau )]=\sum _{\tau =0}^{t}V(\tau ,x)$.

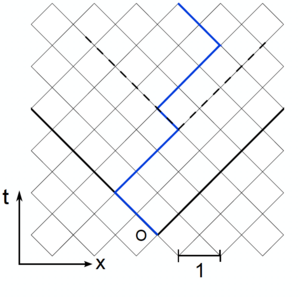
We introduce a lattice model for the directed polymer (see figure). In a companion notebook we provide the implementation of the powerful Dijkstra algorithm.

Dijkstra allows to identify the minimal energy among the exponential number of configurations $x(\tau )$

$E_{\min }=\min _{x(\tau )}E[x(\tau )].$

We are also interested in the ground state configuration $x_{\min }(\tau )$. For both quantities we expect scale invariance with two exponents $\theta ,\zeta$ for the energy and for the roughness

$E_{\min }=c_{\infty }t+b_{\infty }t^{\theta }\chi ,\quad x_{\min }(t/2))\sim a_{\infty }t^{\zeta }{\tilde {\chi }}$

Universal exponents: Both $\theta ,\zeta$ are Independent of the lattice, the disorder distribution, the elastic constants, or the boudanry conditions. Note that $\omega =\theta$, while for an interface $\omega =d\theta$.

Non-universal constants: $c_{\infty },b_{\infty },a_{\infty }$ are of order 1 and depend on the lattice, the disorder distribution, the elastic constants... However $c_{\infty }$ is independent on the boudanry conditions!

Universal distributions: $\chi ,{\tilde {\chi }}$ are instead universal, but depends on the boundary condtions. Starting from 2000 a magic connection has been revealed between this model and the smallest eigenvalues of random matrices. In particular I discuss two different boundary conditions:

• Droplet: $x(\tau =0)=x(\tau =t)=0$. In this case, up to rescaling, $\chi$ is distributed as the smallest eigenvalue of a GUE random matrix (Tracy Widom distribution $F_{2}(\chi )$)

• Flat: $x(\tau =0)=0$ while the other end $x(\tau =t)$ is free. In this case, up to rescaling, $\chi$ is distributed as the smallest eigenvalue of a GOE random matrix (Tracy Widom distribution $F_{1}(\chi )$)

Entropy and scaling relation

It is useful to compute the entropy

${\text{Entropy}}=\ln {\binom {t}{\frac {t-x}{2}}}\approx t\ln 1-{\frac {x^{2}}{t}}+O(x^{4})$

From which we infer

$\theta =2\zeta -1$

Back to the continuum model

Let us consider polymers $x(\tau )$ of length $t$, starting in $0$ and ending in $x$ and at thermal equlibrium at temperature $T$. The partition function of the model writes as

$Z(x,t)=\int _{x(0)=0}^{x(t)=x}{\cal {D}}x(\tau )\exp \left[-{\frac {1}{T}}\int _{0}^{t}d\tau {\frac {1}{2}}(\partial _{\tau }x)^{2}+V(x(\tau ),\tau )\right]$

We remark that the energy of the polymer is equivalent to the euclidean action of a particle. Indeed $\tau =it'$ is the imaginary time. Hence, the term $-{\frac {1}{2}}(\partial _{\tau }x)^{2}$ is the kinetic energy and $V(x(\tau ),\tau )$ is a time dependent potential. For simplicity, we assume a white noise, ${\overline {V(x,\tau )V(x',\tau ')}}=D\delta (x-x')\delta (\tau -\tau ')$.

Within this analogy, $Z[x,t]$, is the propagator of a quantum particle, but in the imaginary time (as $i/\hbar \int dt'$ is replaceed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/T \int d \tau} ). Hence, in absence of disorder we recover the diffusion propagator of the free particle.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{\text{free}}(x,t)=\frac{e^{-x^2/(2Tt)}}{\sqrt{2Tt}} }

Feynman-Kac foruma

Let's derive the Feyman Kac formula for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z(x,t)} in the general case:

• First, focus on free paths and introduce the following probability

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P[A,x,t] =\int_{x(0)=0}^{x(t)=x} {\cal D} x(\tau) \exp\left[- \frac{1}{T} \int_0^t d \tau \frac{1}2(\partial_\tau x)^2 \right] \delta\left( \int_0^t d \tau V(x(\tau),\tau)-A \right) }

• Second, the moments generating function

$Z_{p}(x,t)=\int _{-\infty }^{\infty }dAe^{-pA}P[A,x,t]=\int _{x(0)=0}^{x(t)=x}{\cal {D}}x(\tau )e^{-{\frac {1}{T}}\int _{0}^{t}d\tau {\frac {1}{2}}(\partial _{\tau }x)^{2}-p\int _{0}^{t}d\tau V(x(\tau ),\tau )}$

• Third, the backward approach. Consider free paths evolving up to $t+dt$ and reaching $x$ :

$Z_{p}(x,t+dt)=\left\langle e^{-p\int _{0}^{t+dt}d\tau V(x(\tau ),\tau )}\right\rangle =\left\langle e^{-p\int _{0}^{t}d\tau V(x(\tau ),\tau )}\right\rangle e^{-pV(x,t)dt}=[1-pV(x,t)dt+\dots ]\left\langle Z_{p}(x-\Delta x,t)\right\rangle _{\Delta x}$

Here $\langle \ldots \rangle$ is the average over all free paths, while $\langle \ldots \rangle _{\Delta x}$ is the average over the last jump, namely $\langle \Delta x\rangle =0$ and $\langle \Delta x^{2}\rangle =Tdt$.

• At the lowest order we have

$Z_{p}(x,t+dt)=Z_{p}(x,t)+dt\left[{\frac {T}{2}}\partial _{x}^{2}Z_{p}-pV(x,t)Z_{p}\right]+O(dt^{2})$

Replacing $p=1/T$ we obtain the partition function is the solution of the Schrodinger-like equation:

$\partial _{t}Z=-{\hat {H}}Z={\frac {T}{2}}{\frac {d^{2}Z}{dx^{2}}}-{\frac {V(x,\tau )}{T}}Z$

The initial condition is $Z[x,t=0]=\delta (x)$. This equation is a diffusive equation with multiplicative noise. The EW of the previous lecture is a diffusive equation with additive noise. The Cole Hopf transformation allows to map the diffusive equation with multiplicative noise in a non-linear equation with additive noise: the KPZ euqation. Hence, all KPZ results can be used for the directed polymer.

Cole Hopf Transformation

Replacing

• $T=2\nu$
• $Z[x_{t},t;0,0]=\exp \left({\frac {\lambda }{2\nu }}h(x,t)\right)$
• $-V(x,t)=\lambda \eta (x,t)$

You get

$\partial _{t}h(r,t)=\nu \nabla ^{2}h(r,t)+{\frac {\lambda }{2}}(\nabla h)^{2}+\eta (r,t)$

The KPZ equation! We can establish a KPZ/Directed polymer Dictionary

Dictionary

KPZ	KPZ exponents	Directed polymer	Directed polymer exponents
$r$	$r\sim t^{1/z}$	$x$	$x\sim t^{\zeta }$
$t$	$h(r,t)\sim t^{\alpha /z}$	$t$
$h$	$h(r,t)\sim r^{\alpha }$	$F,E_{\min }$	${\overline {(E_{\min }-{\overline {E_{\min }}})}}^{2}\sim t^{2\theta }$

Here $F$ is the free energy of the directed polymer. At low temperature, the free energy approaches the ground state energy, $E_{\min }$. This dictionary is valid in any dimension. We conclude that

$\theta =\alpha /z,\quad \zeta =1/z$

Moreover, the scaling relation $\theta =2\zeta -1$ is a reincarnation of the Galilean invariance $\alpha +z=2$.