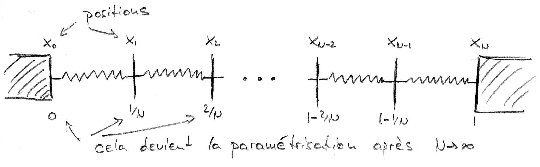T-II-2

Variational methods

Elastic line

During the class you determined the shape of an non-extensible string in a gravitational potential. Here, we study a different situation: the case of an elastic line. Hooke's law states that Elastic energy is proportional to the square of the global elongation.

Elasticity

We write in two Step the elastic energy of a string with an elastic constant $k$. The shape of the string is defined by the function $y(x)$, where $0<x<1$ and $y(0)=y(1)=0$.

Step one: the discrete model

• Write the elastic energy of a chain of N identical springs as a function of their position $y_1,y_2,\dots ,y_N$ (See figure).
• Determine the elastic constant of each spring in order to have a string with an elastic constant $k$

Step two: The continuum limit

• Take the limit $N\to \mathrm{\infty }$ and express the elastic energy as a functional of $y(x)$. (Input: use $1/N\to \text{d}x$ and $\frac{y_{i+1}-y_i}{1/N}\to \frac{\text{d}y(x)}{\text{d}x}$)

Gravity

We write now the gravitational potential as a functional of $y(x)$. We will use two different methods. We suppose that the total mass of the line in $M$.

• Suppose that springs are massless and $N$ identical masses are located at positions $y_1,y_2,\dots$

• Combine your finding for elasticity and gravity and show that the shape of the elastic line is parabolic

Dynamics

We want to study the motion of the elastic line in absence of gravity and in presence of small oscillations. The shape of the line is now time dependent $y(x,t)$.

• Write the kinetic energy associated to the $N$ masses located at $y_1(t),y_2(t),\dots ,y_N(t)$. Take the continuum limit.

The action associated to the elastic chain is

$\underset{t_1}{\overset{t_2}{\int }}dt\underset{0}{\overset{1}{\int }}dx{ℒ}(x,t)$

where ${ℒ}(x,t)$ is the Lagrangian denisty

• Write explicitly ${ℒ}(x,t)$ .
• Write the equation of motion of the chain using the minimum action principle. This equation is the D'Almbert equation.

Sound waves in ideal gas

Consider a uniform ideal gas of equilibrium mass density ${\rho }_0$ and equilibrium pressure $P_0$. Let us investigate the longitudinal oscillations of such a gas. Of course, these oscillations are usually referred to as sound waves.

Kinetic Energy

In a first time we can start from the discrete description of a system of N atoms at positions ${\overrightarrow{u}}_1(t),{\overrightarrow{u}}_2(t),\dots ,{\overrightarrow{u}}_N(t)$.

• Write the kinetic energy, $T$, for this system as a function of mass of the atom $m$.
• Consider the limit of small oscillations. Take the continuum limit: ${\overrightarrow{u}}_i(t)\to \overrightarrow{u}(\overrightarrow{r},t)$ and show that the kinetic energy writes

$T=\frac{{\rho }_0}{2}\int d\overrightarrow{r}{\dot{\overrightarrow{u}}}^2(\overrightarrow{r},t)$

Potential Energy

In order to write the full Lagrangian we need to find the potential energy associated to the oscillations. During the oscillations the mass density can have small fluctuations

$\rho (\overrightarrow{r},t)={\rho }_0+\delta \rho (\overrightarrow{r},t)={\rho }_0(1+\sigma (\overrightarrow{r},t))$

The scalar field $\sigma (\overrightarrow{r},t)$ represents the relative fluctuation of the density.

As a consequence of these fluctuations, the volume which contains a given mass $M$ expands from the initial value $V_0$ to a new value $V_0+\delta V$. The pressure inside the domain also fluctuates $P=P_0+\dots$. The variation of potential energy is given by the work associated to the volume expansion:

$V_0{𝒱}(\overrightarrow{r},t)-\underset{V_0}{\overset{V_0+\delta V}{\int }}Pd\overrightarrow{r}=-P_0\delta V-\frac{1}{2}{\left(\frac{\partial P}{\partial V}\right)}_0\delta V^2+\dots$

where ${𝒱}(\overrightarrow{r},t)$is the density of potential energy.

Generally speaking, a sound wave in an ideal gas oscillates sufficiently rapidly that heat is unable to flow fast enough to smooth out any temperature perturbations generated by the wave. Under these circumstances, the gas obeys the adiabatic gas law,

$P{V}^{\gamma }=$ constant

where $\gamma$ the ratio of specific heats (i.e., the ratio of the gas's specific heat at constant pressure to its specific heat at constant volume). This ratio is approximately $1.4$ for ordinary air.

• Show that the total potential energy, $W=\int d\overrightarrow{r}{𝒱}(\overrightarrow{r},t)$ writes

$W=P_0\int d\overrightarrow{r}(\sigma +\frac{\gamma }{2}{\sigma }^2)$

• Using the continuity equation of the gas, ${\partial }_t\rho =-{\rho }_0\overrightarrow{\mathrm{\nabla }}\cdot {\partial }_t\overrightarrow{u}(\overrightarrow{r},t)$, show that $\sigma (\overrightarrow{r},t)=-\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}(\overrightarrow{r},t)$ and write the potential energy as a function of $\overrightarrow{u}(\overrightarrow{r},t)$

Lagrangian description

• Show that the Lagrangian density writes

${ℒ}(\overrightarrow{r},t)=\frac{{\rho }_0}{2}{\dot{\overrightarrow{u}}}^2+P_0\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}-\frac{\gamma }{2}{P}_0(\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}{)}^2$

• Show that the associated equation of motion

${\rho }_0\frac{{\partial }^2\overrightarrow{u}}{\partial t^2}-\gamma P_0\overrightarrow{\mathrm{\nabla }}\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}=0$

• Using the continuity relation $\sigma =-\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}$ show that the latter equation corresponds to the D'Alembert Equation for the scalar field $\sigma$

This scalar field behaves exaclty like an elastic scalar field.

• Determine the sound velocity.