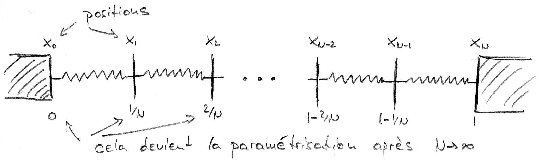T-II-2

From ESPCI Wiki
Jump to navigation Jump to search


Variational methods

Elastic line

During the class you determined the shape of an non-extensible string in a gravitational potential. Here, we study a different situation: the case of an elastic line. Hooke's law states that Elastic energy is proportional to the square of the global elongation.


Elasticity

Image009.jpg Image008.jpg

We write in two Step the elastic energy of a string with an elastic constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } . The shape of the string is defined by the function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x) } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<x <1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(0)=y(1)=0} .


Step one: the discrete model

  • Write the elastic energy of a chain of N identical springs a a function of their position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1, y_2,\ldots,y_N } (See figure).
  • Determine the elastic constant of each spring in order to have a a string with an elastic constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k }

Step two: The continuum limit

  • Take the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \to \infty} and express the elastic energy as a functional of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x) } . (Input: use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/N \to \text{d} x} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{y_{i+1}-y_i}{1/N} \to \frac{\text{d} y(x)}{\text{d} x }} )

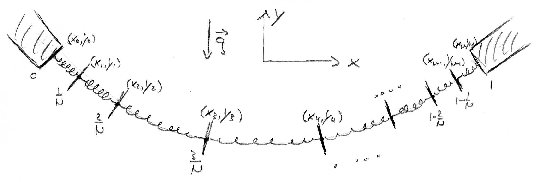
Gravity

We write now the gravitational potential as a functional of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x)} . We will use two different methods. We suppose that the total mass of the line in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} .

  • Suppose that springs are massless and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} identical masses are located at positions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1,y_2,\ldots}
  • Combine your finding for elasticity and gravity and show that the shape of the elastic line is parabolic

Dynamics

We want to study the motion of the elastic line in absence of gravity and in presence of small oscillations. The shape of the line is now time dependent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x,t)} .

  • Write the kinetic energy associated to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } masses located at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1(t),y_2(t),\ldots, y_N(t) } . Take the continuum limit.

The action associated to the elastic chain is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{t_1}^{t_2} d t \int_0^1 d x \, \mathcal{L} (x,t) }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal L}(x,t) } is the Lagrangian denisty

  • Write explicitly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal L}(x,t) } .
  • Write the equation of motion of the chain using the minimum action principle. This equation is the D'Almbert equation.

Sound waves in ideal gas

Consider a uniform ideal gas of equilibrium mass density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0 } and equilibrium pressure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_0} . Let us investigate the longitudinal oscillations of such a gas. Of course, these oscillations are usually referred to as sound waves.

Kinetic Energy

In a first time we can start from the discrete description of a system of N atoms at positions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\vec u}_1(t), {\vec u}_2(t) ,\ldots , {\vec u}_N(t) } .

  • Write the kinetic energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } , for this system as a function of mass of the atom Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } .
  • Consider the limit of small oscillations. Take the continuum limit: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\vec u}_i(t) \to \vec u(\vec r,t) } and show that the kinetic energy writes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T= \frac{\rho_0}{2} \int \, d \vec{r} \, \dot{\vec{u}}^2 (\vec r,t) }

Potential Energy

In order to write the full Lagrangian we need to find the potential energy associated to the oscillations. During the oscillations the mass density can have small fluctuations

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(\vec r,t)=\rho_0+\delta \rho(\vec r,t)=\rho_0\left( 1+\sigma(\vec r,t)\right)}

The scalar field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma(\vec r,t)} represents the relative fluctuation of the density.

As a consequence of these fluctuations, the volume which contains a given mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M } expands from the initial value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0 } to a new value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0 +\delta V} . The pressure inside the domain also fluctuates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P=P_0+\ldots } . The variation of potential energy is given by the work associated to the volume expansion:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0 {\mathcal{V}} - \int_{V_0}^{V_0+\delta V} \, P\, d \vec{r}=-P_0 \delta V- \frac{1}{2} \left( \frac{\partial P }{\partial V}\right)_0 \delta V^2+\ldots }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal V} is the density of potential energy.

Generally speaking, a sound wave in an ideal gas oscillates sufficiently rapidly that heat is unable to flow fast enough to smooth out any temperature perturbations generated by the wave. Under these circumstances, the gas obeys the adiabatic gas law,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P V^\gamma= } constant

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} the ratio of specific heats (i.e., the ratio of the gas's specific heat at constant pressure to its specific heat at constant volume). This ratio is approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.4 } for ordinary air.

  • Show that the total potential energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=\int \, d \vec{r} \, \mathcal V} writes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W= P_0 \int \, d \vec{r} \, \left( \sigma + \frac{\gamma}{2} \sigma^2\right) }
  • Using the continuity equation of the gas show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma(\vec{r},t)= - \vec{\nabla} \cdot \vec{u}(\vec{r},t) } and write the potential energy as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}(\vec{r},t) }

Lagrangian description

  • Show that the Lagrangian density writes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L} (\vec{r},t) = \frac{\rho_0}{2} \dot{\vec{u}}^2 + P_0 \vec{\nabla} \cdot \vec{u} -\frac{\gamma}{2} P_0 (\vec{\nabla} \cdot \vec{u})^2 }
  • Show that the associated equation of motion
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0 \frac{\partial^2 \vec{u}}{\partial t^2} -\gamma P_0 \vec{\nabla} \vec{\nabla} \cdot \vec{u}=0 }
  • Using the continuity relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma= - \vec{\nabla} \cdot \vec{u} } show that the latter equation corresponds to the D'Alembert Equation for the scalar field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma }

This scalar field behaves exaclty like an elastic scalar field.

  • Determine the sound velocity.
Retrieved from "http://www.lptms.universite-paris-saclay.fr//wikiespci/index.php?title=T-II-2&oldid=205"