T-4

Goal: understand the information encoded in the replica solution, and the difference between Replica Symmetry (RS) and Replica Symmetry Breaking (RSB).
Techniques: replica method, variational ansatz, saddle point approximation.

The overlaps, and why they tell us about glassiness

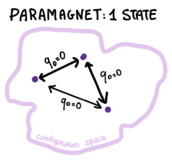
• Order parameter, ergodicity-breaking, states: the ferromagnet. The order parameter for ferromagnets is the magnetization:

  $m=\lim _{h\to 0}\lim _{N\to \infty }{\frac {1}{N}}\sum _{i=1}^{N}{\overline {\langle \sigma _{i}\rangle _{h}}}$

  where $\langle \cdot \rangle _{h}$ is the Boltzmann average in presence of a magnetic field $h$, and the average over the disorder can be neglected because this quantity is self-averaging. Notice the order of limits: first the thermodynamic limit, and then the limit of zero field.

  A non-zero magnetisation is connected to ergodicity breaking. When ergodicity is broken, the Boltzmann measure clusters into pure states (labelled by $\alpha$) with weight $\omega _{\alpha }$, meaning that one can re-write the thermal averages $\langle \cdot \rangle$ of any observable $A$ as

  $\langle A\rangle =\sum _{\alpha }\omega _{\alpha }\langle A\rangle _{\alpha },\quad \quad \quad \omega _{\alpha }={\frac {Z_{\alpha }}{Z}},\quad \quad \quad Z_{\alpha }=\int _{{\vec {\sigma }}\in {\text{ state }}\alpha }d{\vec {\sigma }}e^{-\beta E({\vec {\sigma }})}=\langle e^{-\beta E({\vec {\sigma }})}\rangle _{\alpha }$

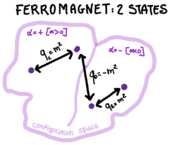
  In the ferromagnet there are two pure states, $\alpha =\pm 1$, that correspond to positive and negative magnetization. These two states are related by symmetry. A small field $h$ selects one of them (symmetry breaking).



• Order parameter, ergodicity-breaking, states: the glass. In Lecture 1, we have introduced the Edwards-Anderson order parameter as: $q_{EA}=\lim _{t\to \infty }\lim _{N\to \infty }{\frac {1}{N}}\sum _{i}\sigma _{i}(0)\sigma _{i}(t)$

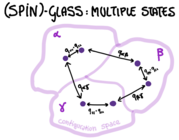
  This measures the autocorrelation between the configuration of the same spin at $t=0$ and that at infinitely larger time. A non-zero value of $q_{EA}$ is again an indication of ergodicity breaking: if there was not ergodicity breaking, the system would be able to visit dynamically all configurations according to the Boltzmann measure, decorrelating to the initial condition. The fact that $q_{EA}>0$ indicates that the system, even at later times, is constrained to visit configurations that are not too different from the initial ones: this is because it explores only one of the available pure states! The difference with the ferromagnets is that in mean-field glassy models like the spherical $p$-spin, there are not just two but several different states, not related by symmetry.
  

  The quantity $q_{EA}$ measures the overlap between configurations in the same state, that one expects to be the same for all states. In a thermodynamics formalism, it can be written as ^[*]

  $q_{EA}=q_{\alpha \alpha }=\lim _{N\to \infty }{\frac {1}{N}}\sum _{i}\langle \sigma _{i}\rangle _{\alpha }\langle \sigma _{i}\rangle _{\alpha }$

  Notice that this non-zero in a spin-glass phase, but it is also different from zero in unfrustrated ferromagnets: in the low-T phase of an Ising model, it equals to $m^{2}$, where $m$ is the magnetization.


• Replica formalism: where is this info encoded? The overlap between configurations in different states is accounted for by the overlap distribution:

  $q_{\alpha \beta }={\frac {1}{N}}\sum _{i}\langle \sigma _{i}\rangle _{\alpha }\langle \sigma _{i}\rangle _{\beta },\quad \quad \quad {P}_{\beta ,N}(q)=\sum _{\alpha ,\beta }\omega _{\alpha }\,\omega _{\beta }\,\delta (q-q_{\alpha \beta }).$

  The average value of this distribution (when $N\to \infty$) can be computed within the replica formalism, and one finds:

  ${\overline {{P}_{\beta }(q)}}:=\lim _{N\to \infty }{\overline {P_{\beta ,N}(q)}}=\lim _{n\to 0}{\frac {2}{n(n-1)}}\sum _{a<b}\delta \left(q-q_{ab}^{*}\right),\quad \quad \quad q_{EA}=\max _{a<b}\left\{q_{ab}^{*}\right\}$

  where $q_{ab}^{*}$ are the saddle point values of the overlap matrix. In the Ising case, a low temperature one has $q_{\alpha \alpha }=m^{2}$ and $q_{\alpha \neq \beta }=-m^{2}$, and thus ${P}_{\beta }(q)$ has two peaks at $\pm m^{2}$. In spin-glass models, the structure of the distribution can be more complicated.

[*] - To be precise, in analogy with the magnetization, we should write $q_{EA}=\lim _{\epsilon \to 0}\lim _{N\to \infty }{\frac {1}{N}}\sum _{i}\langle \sigma _{i}^{1}\,\sigma _{i}^{2}\rangle _{\epsilon }$, where ${\vec {\sigma }}^{1},{\vec {\sigma }}^{2}$ are two copies of the system, and the average is with respect to a tilted Boltzmann measure which contains a small coupling $\epsilon$ between them, which plays the same role of the infinitesimal magnetic fields in the ferromagnet. The coupling is so weak that it only forces the configurations to fall in the same pure state, but a part from this it leaves them independent.

Problems

We go back to the spherical $p$-spin model, and complete the calculation of the free energy under different assumptions on the structure of the overlap matrix.

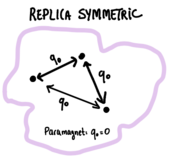
Problem 4.1: the RS (Replica Symmetric) solution

We go back to the saddle point equations for the spherical $p$-spin model derived in the previous problems. Let us consider the simplest possible ansatz for the structure of the matrix Q, that is the Replica Symmetric (RS) ansatz:

$Q={\begin{pmatrix}1&q_{0}&q_{0}\cdots &q_{0}\\q_{0}&1&q_{0}\cdots &q_{0}\\&\cdots &&\\q_{0}&q_{0}&q_{0}\cdots &1\end{pmatrix}}$

Under this assumption, there is a unique saddle point variable, that is $q_{0}$. We denote with $q_{0}^{*}$ its value at the saddle point.

1. RS overlap distribution. Under this assumption, what is the overlap distribution ${\overline {P_{\beta }(q)}}$ and what is $q_{EA}$? In which sense the RS ansatz corresponds to assuming the existence of a unique pure state?

2. RS free energy. Show that the saddle point equation for $q_{0}$ when $n\to 0$ is

   $\beta ^{2}\,pq_{0}^{p-1}-{\frac {q_{0}}{(1-q_{0})^{2}}}=0,$

   which admits always the solution $q_{0}^{*}=0$: why is this called the paramagnetic solution? Show that within this RS assumption, the quenched free energy coincides with the annealed one.

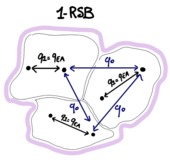
Problem 4.2: the 1-RSB (Replica Symmetry Broken) calculation

In the previous problem, we have chosen a certain parametrization of the overlap matrix $Q$, which corresponds to assuming that typically all the copies of the systems fall into configurations that are at overlap $q_{0}$ with each others, no matter what is the pair of replicas considered. This assumption is however not the good one at low temperature. We now assume a different parametrisation, that corresponds to breaking the symmetry between replicas: in particular, we assume that typically the $n$ replicas fall into configurations that are organized in $n/\mu$ groups of size $\mu$ (replicas in the same group are equilibrating in the same pure state); pairs of replicas in the same group are more strongly correlated and have overlap $q_{1}$, while pairs of replicas belonging to different groups have a smaller overlap $q_{0}<q_{1}$. This corresponds to the following block structure for the overlap matrix:

$Q={\begin{pmatrix}1&q_{1}&q_{1}&q_{0}&q_{0}\cdots &q_{0}\\q_{1}&1&q_{1}&q_{0}&q_{0}\cdots &q_{0}\\q_{1}&q_{1}&1&q_{0}&q_{0}\cdots &q_{0}\\\cdots \\\cdots \\\cdots \\q_{0}&q_{0}\cdots &q_{0}&1&q_{1}&q_{1}\\q_{0}&q_{0}\cdots &q_{0}&q_{1}&1&q_{1}\\q_{0}&q_{0}\cdots &q_{0}&q_{1}&q_{1}&1\\\end{pmatrix}}$

Here we have three parameters: $\mu ,q_{0},q_{1}$ (in the sketch above, $\mu =3$). We denote with $\mu ^{*},q_{0}^{*},q_{1}^{*}$ their values at the saddle point.

1. 1-RSB overlap distribution. Show that in this case the overlap distribution is

   ${\overline {P_{\beta }(q)}}=\mu ^{*}\delta (q-q_{0}^{*})+(1-\mu ^{*})\delta (q-q_{1}^{*})$

   What is $q_{EA}$? In which sense the parameter $\mu$ when $n\to 0$ can be interpreted as a probability weight?

2. 1-RSB free energy and saddle point equations. Under the 1RSB assumption, the expression for the free energy is:

   $f_{1RSB}=-{\frac {1}{2\beta }}\left[\beta ^{2}\left(1+(\mu -1)q_{1}^{p}-\mu q_{0}^{p}\right)+{\frac {\mu -1}{\mu }}\log(1-q_{1})+{\frac {1}{\mu }}\log[\mu (q_{1}-q_{0})+1-q_{1}]+{\frac {q_{0}}{\mu (q_{1}-q_{0})+1-q_{1}}}\right]{\Big |}_{q_{1}^{*},q_{0}^{*},\mu ^{*}}$

   Under which limit one recovers the the replica symmetric ansatz? Compute the saddle point equations with respect to the parameter $q_{0},q_{1}$ and $\mu$. Check that $q_{0}=0$ is again a valid solution of these equations, and that for $q_{0}=0$ the remaining equations reduce to:

   $(\mu -1)\left[\beta ^{2}\,pq_{1}^{p-1}-{\frac {1}{\mu }}{\frac {1}{1-q_{1}}}+{\frac {1}{\mu }}{\frac {1}{1+(\mu -1)q_{1}}}\right]=0,\quad \quad \beta ^{2}\,q_{1}^{p}+{\frac {1}{\mu ^{2}}}\log \left({\frac {1-q_{1}}{1+(\mu -1)q_{1}}}\right)+{\frac {q_{1}}{\mu [1+(\mu -1)q_{1}]}}=0$

3. The "random first-order" transition. One solution to the saddle point equations is $\mu ^{*}=1$ and $q_{0}^{*}=0=q_{1}^{*}$. This is the only good solution one finds at high temperature. However, at a given critical temperature $T_{c}$ one finds that the system of equations is still solved by $\mu ^{*}=1$, but the equation for $q_{1}$

   $\beta ^{2}\,q_{1}^{p}+\log \left(1-q_{1}\right)+q_{1}=0$

   develops a new solution at a $q_{1}^{*}\neq 0$: try to estimate this temperature numerically by plotting this function for $p=3$ and different values of $\beta$, and check that $\beta _{c}\approx 1.2066$. When $T$ decreases below $T_{c}$, one sees that $\mu ^{*}$ becomes smaller than one, and $q_{1}^{*}$ increases towards one. What is different and what is similar with respect to the REM?

Replica Symmetry Breaking: the Parisi scheme

For the spherical $p$-spin model, the low-T phase is glassy and the description within a 1-RSB ansatz is exact: the equilibrium in the glassy phase is described by three quantities: the typical overlap $q_{1}^{*}$ between configurations belonging to the same state, the typical overlap $q_{0}^{*}$ between configurations belonging to different states, and the probability $(1-\mu ^{*})$ that two configurations extracted at equilibrium belong to the same state.

There are models for which the glassy phase is described by a more complicated pattern of the mutual overlaps between states, which is obtained iterating the RSB scheme to $K$ levels, ending up with a series of overlaps $q_{K}>q_{K-1}>\cdots >q_{0}$. The underlying picture of the free-energy landscape is as follows: configurations in the same pure state have typical overlap $q_{K}=q_{EA}$. They are arranged in clusters such that configurations belonging to different states inside a cluster have overlap $q_{K-1}$, but such clusters are arranged in other clusters at a higher level, at mutual overlap $q_{K-2}$ and so on.

The exact solution of the Sherrington-Kirkpatrick model introduced in Lecture 1 is obtained iterating this procedure an infinite number of times ($K\to \infty$): this is the full-RSB solution. In this limit, the overlap distribution is continuous. The intuition that the free-energy landscape in mean-field spin glasses has this hierarchical structure is due to Giorgio Parisi. Both 1RSB and fullRSB features are found in mean-field models of structural glasses [5].

Check out: key concepts

Order parameters, ergodicity breaking, pure states, overlaps, overlap distribution, replica-symmetric ansatz, replica symmetry breaking.

To know more

• A note on Elisabeth Garder [1]
• Castellani, Cavagna. Spin-Glass Theory for Pedestrians [2]
• Zamponi. Mean field theory of spin glasses [3]
• Parisi. Order parameter for spin-glasses [4]
• Urbani. Statistical Physics of glassy systems: tools and applications [5]