L-2

Goal: The physical properties of many materials are controlled by the interfaces embedded in it. This is the case of the dislocations in a crystal, the domain walls in a ferromagnet or the vortices in a supercoductors. In the next lecture we will discuss how impurities affect the behviour of these interfaces. Today we focus on thermal fluctuations and introduce two important equations for the interface dynamics: the Edwards Wilkinson (EW) and the Kardar Parisi Zhang (KPZ) equations.

Interfaces: thermal shaking

Consider domain wall $h(r,t)$ fluctuating at equilibrium at the temperature $T$. Here $t$ is time, $r$ defines the d-dimensional coordinate of the interface and $h$ is the scalar height field. Hence, the domain wall separating two phases in a film has $d=1,r\in {\cal {R}}$, in a solid instead $d=2,r\in {\cal {{R}^{2}}}$.

Two assumptions are done:

• Overhangs, pinch-off are neglected, so that $h(r,t)$ is a scalar univalued function.
• The dynamics is overdamped, so that we can neglect the inertial term.

Derivation

The Langevin equation of motion is

$\partial _{t}h(r,t)=-\mu {\frac {\delta E_{pot}}{\delta h(r,t)}}+\eta (r,t)$

The first term $-\delta E_{pot}/\delta h(r,t)$ is the elastic force trying to smooth the interface, the mobility $\mu$ is the inverse of the viscosity. The second term is the Langevin noise. It is Guassian and defined by

$\langle \eta (r,t)\rangle =0,\;\langle \eta (r',t')\eta (r,t)\rangle =2dD\delta ^{d}(r-r')\delta (t-t')$

The symbol $\langle \ldots \rangle$ indicates the average over the thermal noise and the diffusion constant is fixed by the Einstein relation $D=\mu K_{B}T$. We set $\mu =K_{B}=1$

The potential energy of surface tension ($\nu$ is the stiffness) can be expanded at the lowest order in the gradient:

$E_{pot}=\nu \int d^{d}r{\sqrt {1+(\nabla h)^{2}}}\sim {\text{const.}}+{\frac {\nu }{2}}\int d^{d}r(\nabla h)^{2}$

Hence, we have the Edwards Wilkinson equation:

$\partial _{t}h(r,t)=\nu \nabla ^{2}h(r,t)+\eta (r,t)$

Scaling Invariance

The equation enjoys of a continuous symmetry because $h(r,t)$ and $h(r,t)+c$ cannot be distinguished. This is a condition of scale invariance:

$h(br,b^{z}t){\overset {inlaw}{\sim }}b^{\alpha }h(r,t)$

Here $z,\alpha$ are the dynamic and the roughness exponent respectively. From dimensional analysis

$b^{\alpha -z}\partial _{t}h(r,t)=b^{\alpha -2}\nabla ^{2}h(r,t)+b^{-d/2-z/2}\eta (r,t)$

From which you get $z=2$ in any dimension and a rough interface below $d=2$ with $\alpha =(2-d)/2$.

Exercise L2-A: Solve Edwards-Wilkinson

For simplicity, consider a 1-dimensional line of size L with periodic boundary conditions. It is useful to introduce the Fourier modes:

${\hat {h}}_{q}(t)={\frac {1}{L}}\int _{0}^{L}e^{iqr}h(r,t),\quad h(r,t)=\sum _{q}e^{-iqr}{\hat {h}}_{q}(t)$

Here $q=2\pi n/L,n=\ldots ,-1,0,1,\ldots$ and recall $\int _{0}^{L}dre^{iqr}=L\delta _{q,0}$.

• Show that the EW equation writes

$\partial _{t}{\hat {h}}_{q}(t)=-\nu q^{2}{\hat {h}}_{q}(t)+\eta _{q}(t),\quad {\text{with}}\;\langle \eta _{q_{1}}(t')\eta _{q_{2}}(t)\rangle ={\frac {2T}{L}}\delta _{q_{1},-q_{2}}\delta (t-t')$

The solution of this first order linear equation writes

${\hat {h}}_{q}(t)={\hat {h}}_{q}(0)e^{-\nu q^{2}t}+\int _{0}^{t}dse^{-\nu q^{2}(t-s)}\eta _{q}(s)$

Assume that the interface is initially flat, namely ${\hat {h}}_{q}(0)=0$.

• Compute the width $\langle h(x,t)^{2}\rangle =\sum _{q}\langle h_{q}(t)h_{-q}(t)\rangle$. Comment about the roughness and the short times growth.

KPZ equation and interface growth

Consider a domain wall in presence of a positive magnetic field. At variance with the previous case the ferromagnetic domain aligned with the field will expand while the other will shrink. The motion of the interface describes now the growth of the stable domain, an out-of-equilibrium process.

Derivation

The growth is normal (orthogonal) to the interface.

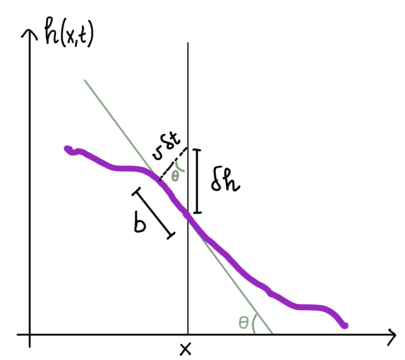
To derive the correct equation of a growing interface the key point is to realize that the growth occurs locally along the normal to the interface (see figure).

Let us call $v$ the velocity of the interface. Consider a point of the interface $h(r,t)$, its tangent is $\partial _{r}h(r,t)=-\tan(\theta )$. To evaluate the increment $\delta h(r,t)$ use the Pitagora theorem:

$\delta h(r,t)={\sqrt {(vdt)^{2}+(vdt\tan(\theta ))^{2}}}\sim vdt+{\frac {vdt}{2}}(\tan(\theta ))^{2}\sim vdt+{\frac {vdt}{2}}(\partial _{r}h(r,t))^{2}$

Hence, in generic dimension, the KPZ equation is

$\partial _{t}h(r,t)=\nu \nabla ^{2}h(r,t)+{\frac {\lambda }{2}}(\nabla h)^{2}+\eta (r,t)$

Scaling Invariance

The symmetry $h$ and $h+c$ still holds so that scale invariance is still expected. However the non-linearity originate an anomalous dimension and $z,\alpha$ cannot be determined by simple dimensional analysis.

An important symmetry

Let us remark that if $h(r,t)$ is a solution of KPZ,also ${\tilde {h}}(r,t)=h(r+\lambda v_{0}t,t)+v_{0}r+(v_{0}^{2}\lambda /2)t$ is a solution of KPZ, provided the change of variables ${\tilde {r}}=r+\lambda v_{0}t$ . You can check it, and you will obtain an equation with the statistically equivalent noise $\eta ({\tilde {r}}-\lambda v_{0}t,t)$. The symmetry relies on two properties:

• The noise $\eta (r,t)$ is delta correlated in time
• Only sticked together the two terms $\partial _{t}h(r,t)$ and ${\frac {\lambda }{2}}(\partial _{r}h(r,t))^{2}$ enjoy the symmetry. Hence, under the rescaling

$b^{\alpha -z}\left(\partial _{t}h(r,t)-b^{\alpha +z-2}{\frac {\lambda }{2}}(\partial _{r}h(r,t))^{2}\right)$

the second term should be $b$-independent. This provides a new and exact scaling relation

$z+\alpha =2$

The d=1 case

In the one dimensional case the KPZ equation writes Hence, in generic dimension, the KPZ equation is

$\partial _{t}h(r,t)=\nu \partial _{r}^{2}h(r,t)+{\frac {\lambda }{2}}(\partial _{r}h)^{2}+\eta (r,t)$

The corresponding Fokker Planck equation for the probability ${\cal {P}}[h,t]$ can be written as

$\partial _{t}{\cal {P}}=-\int dr{\frac {\delta }{\delta h_{r}}}\left\{\left[\nu \partial _{r}^{2}h+{\frac {\lambda }{2}}(\partial _{r}h)^{2}\right]{\cal {P}}\right\}+T\int dr{\frac {\delta ^{2}{\cal {P}}}{\delta h_{r}^{2}}}$

The probability

${\cal {P}}_{st}[h]\propto \exp \left\{-{\frac {1}{T}}\int dr\;{\frac {\nu }{2}}(\partial _{r}h)^{2}\right\}$

is a stationary solution (namely $\partial _{t}{\cal {P}}_{st}[h]=0$ )for EW as you can check

$T{\frac {\delta {\cal {P}}_{st}}{\delta h_{r}}}-\nu \partial _{r}^{2}h{\cal {P}}_{st}=0$

It is also a solution (only for $d=1$)

$\int dr{\frac {\delta }{\delta h_{r}}}\left[{\frac {\lambda }{2}}(\partial _{r}h)^{2}{\cal {P}}_{st}\right]=0$

even if the last equality has some issues of disretization. As a conclusion in $d=1$ we have $\alpha =1/2$ as for EW, but $z=3/2$.