T-8

Goal: the goal of this set of problems is to derive a criterion for localization on a peculiar lattice, the Bethe lattice.
Techniques: green functions, recursion relations, cavity method.

A criterion for localization: vanishing decay rate

• Anderson model and return probability. Consider a lattice with $N$ sites $x$. We call $|x⟩$ the wave function completely localised in site $x$. The Anderson model has Hamiltonian:

  $H=W\sum _x{V}_x|x⟩⟨x|-\sum _{<x,y>}{t}_{xy}(|x⟩⟨y|+|y⟩⟨x|)$

  where the local fields $V_x$ are random variables, independent and distributed according to some distribution $p(V)$. Usually, the hopping amplitude $t_{xy}=t$ is chosen to be uniform.

  To see whether localization occurs, consider a quantum particle initialised on the site $x_0$ at $t=0$. The return probability amplitude , i.e. the probability amplitude to find the particle on the same site at later time, is

  ${{𝒜}}_{x_0}(t)=\theta (t)⟨x_0|e^{-itH}|x_0⟩.$

  When the system is not localized, the wave function of the particle spreads in time, and the return probability decays.



• Green functions and self-energies. We introduce two functions on the complex plane: the Green functions $G_{xy}(z)$ and the local self-energies ${\sigma }_x(z)$, where $z=E+i\eta ,\eta >0$ belongs to the upper half of the complex plane. The functions are defined by

  $G_{xy}(z)=⟨x|\frac{1}{z-H}|y⟩,G_{xx}(z)=⟨x|\frac{1}{z-H}|x⟩=\frac{1}{z-V_x-{\sigma }_x(z)}.$

  They are random functions, because the Hamiltonian contains randomness. The Green functions and the self-energies encode properties on the spectrum of the Hamiltonian^[*] , and they are related to the return probability, which can be written as (Laplace transform):

  ${{𝒜}}_{x_0}(t)=\theta (t)⟨x_0|e^{-itH}|x_0⟩=\underset{\eta \to 0}{\lim }\int \frac{dz}{2\pi i}{e}^{-itz}{G}_{x_0{x}_0}(z)=\underset{\eta \to 0}{\lim }\int \frac{dz}{2\pi i}\frac{e^{-itz}}{z-V_{x_0}-{\sigma }_{x_0}(z)}.$



• Anderson's criterion for localization. If the self-energy has a non-zero imaginary part (when $N\to \mathrm{\infty }$):

  ${\sigma }_{x_0}(z)=R_{x_0}(z)-i{\mathrm{\Gamma }}_{x_0}(z),$

  then one can show (How? See here for some notes ) that ${{𝒜}}_{x_0}(t)$ decays exponentially,

  ${{𝒜}}_{x_0}(t)\sim A(t)e^{-\gamma t}+B(t),\gamma ={\mathrm{\Gamma }}_{x_0}(V_{x_0})+O(T^4),$

  and the system is not localized: the probability to find it, at $t\gg 1$, in the same configuration where it was at $t=0$ decays fast. For localization to occur, it must be that the imaginary part of $\sigma x_0(E+i\eta )$ goes to zero when $\eta \to 0$. Given the randomness, this criterion should however be formulated probabilistically:

  $\underset{\eta \to 0}{\lim }\underset{N\to \mathrm{\infty }}{\lim }\mathbb{\mathbb{P}}(-\mathrm{\Im }{\sigma }_{x_0}(E+i\eta )>0)=0⟹\text{Localization}$

  Showing that at strong enough disorder this condition is satisfied is the core of Anderson’s 1958 work.



• A dynamical transition. Notice that in this criterion, the probability plays the role of an order parameter (like the magnetization in ferromagnets, or the average overlap distribution in spin glasses), and the imaginary part $\eta$ plays the role of a symmetry breaking field (like the magnetic field in the ferromagnet, or the coupling between replicas in spin glasses). However, the localization transition has nothing to do with equilibrium, i.e., it is not related to a change of structure of the Gibbs Boltzmann measure; rather, it is a dynamical transition (like depinning!). Pushing the analogy with equilibrium phase transitions, one can say that the localised phase corresponds to the disordered phase (the one in which symmetry is not broken, like the paramagnetic phase).
  

[*] - For example, the local density of eigenvalues ${\nu }_{x,N}(E)$ for an Hamiltonian on a lattice of size $N$ is indeed given by

${\nu }_{x,N}(E)=-\frac{1}{\pi }\underset{\eta \to 0}{\lim }\mathrm{\Im }{G}_{xx}(E+i\eta )=\sum _{\alpha =1}^N|⟨E_{\alpha }|x⟩{|}^2\delta (E-E_{\alpha }),$

where $E_{\alpha }$ are the eigenvalues of the full Hamiltonian $H$ and $|E_{\alpha }⟩$ the corresponding eigenstates. When the kinetic term $T$ in the Hamiltonian vanishes, the local self-energies vanish. They encode how much the energy levels $V_x$ (that are the eigenvalues when $V=0$) are shifted by the presence of the kinetic (hopping) term.

Problems

Problem 8: Bethe lattice, cavity method & recursion relations

A Bethe lattice with $k=2$.

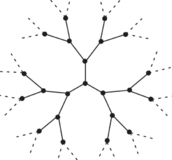
The Bethe lattice is a lattice with a regular tree structure: each node has a fixed number of neighbours $k+1$, where $k$ is the branching number, and there are no loops (see sketch). In these problems we consider the Anderson model on such lattice.

1. Green functions identities. Consider an Hamiltonian split into two parts, $H=H_0+H_1$. Show that the following general relation for the Green functions holds:

   $G=G^0+G^0{H}_{1}G,G^0=\frac{1}{z-H_0},G=\frac{1}{z-H}.$



2. Cavity equations. We now apply this to a specific example: we consider a Bethe lattice, and choose one site 0 as the root. We then choose $H_1$ to be the kinetic terms connecting the root to its $k+1$ neighbors $a_i$,

   $H_1=-\sum _{i=1}^{k+1}{t}_{0a_i}(|a_i⟩⟨0|+|0⟩⟨a_i|)$

   For all the $a_i$ with $i=1,\cdots ,k+1$ we introduce the notation

   $G_{a_i}^{\text{cav}}\equiv G_{a_i{a}_i}^0,{\sigma }_{a_i}^{\text{cav}}\equiv {\sigma }_{a_i}^0,$

   where ${\sigma }^0$ is the self energy associated to $G^0$. Show that, due to the geometry of the lattice, with this choice of $H_1$ the Hamiltonian $H_0$ is decoupled and $G_{a_i}^{\text{cav}}$ is the local Green function that one would have obtained removing the root 0 from the lattice, i.e., creating a “cavity” (hence the suffix). Moreover, using the Green function identities iterated twice, show that

   $G_{00}(z)=\frac{1}{z-W{V}_0-\sum _{i=1}^{k+1}{t}_{0a_i}^2{G}_{a_i}^{\text{cav}}(z)}$

   Iterating this argument, show that if $\partial a_i$ denotes the collection of “descendants" of $a_i$, i.e. sites that are nearest neighbours of $a_i$ except the root, then

   $G_{a_i}^{\text{cav}}(z)=\frac{1}{z-W{V}_{a_i}-\sum _{b\in \partial a_i}{t}_{a_{i}b}^2{G}_b^{\text{cav}}(z)},{\sigma }_{a_i}^{\text{cav}}(z)=\sum _{b\in \partial a_i}{t}_{a_{i}b}^2{G}_b^{\text{cav}}(z)=\sum _{b\in \partial a_i}\frac{t_{a_{i}b}^2}{z-W{V}_b-{\sigma }_b^{\text{cav}}(z)}$



3. Equations for the distribution. Justify why the cavity functions appearing in the denominators in the last equations above are independent and identically distributed random variables, and therefore the cavity equations can be interpreted as self-consistent equations for the distribution of the cavity functions.


4. The “localized" solution. We set $z=E+i\eta$ and ${\sigma }_a^{\text{cav}}(z)=R_a(z)-i{\mathrm{\Gamma }}_a(z)$. Show that the cavity equation for the self-energies is equivalent to the following pair of coupled equations:

   ${\mathrm{\Gamma }}_a=\sum _{b\in \partial a}{t}_{ab}^2\frac{{\mathrm{\Gamma }}_b+\eta }{(E-W{V}_b-R_b{)}^2+({\mathrm{\Gamma }}_b+\eta {)}^2},R_a=\sum _{b\in \partial a}{t}_{ab}^2\frac{E-W{V}_b-R_b}{(E-W{V}_b-R_b{)}^2+({\mathrm{\Gamma }}_b+\eta {)}^2}$

   Justify why the solution corresponding to localization, ${\mathrm{\Gamma }}_a=0$, is always a solution when $\eta \to 0$; moreover, in the localized phase when $\eta$ is finite but small one has ${\mathrm{\Gamma }}_a\sim O(\eta )$. How can one argue that this solution has to be discarded, i.e. that delocalisation occurs?

Check out: key concepts

Green functions, self-energies, return probability amplitude, decay rates, trees and cavity method, the criterion for localization.

References

• The Anderson model was formulated by P. W. Anderson in 1958, in the paper Absence of diffusion in certain random lattices , Phys. Rev. 109, 1492.