T-8: Difference between revisions
| Line 6: | Line 6: | ||
== A criterion for localization: vanishing decay rate== | == A criterion for localization: vanishing decay rate== | ||
<ul> | <ul> | ||
<li> <strong> Anderson model and return probability. </strong> Consider a lattice with <math> N </math> sites <math>x </math>. We call <math> |x \rangle </math> the wave function completely localised in site <math> x </math>. The Anderson model has Hamiltonian: | |||
<center> | |||
<math> | |||
H= W \sum_{x} V_x |x \rangle \langle x| - \sum_{<x, y>} t_{xy} \left(|x \rangle \langle y|+ |y \rangle \langle x| \right)\equiv H_0 + T | |||
</math> | |||
</center> | |||
where the local fields <math> V_x </math> are random variables, independent and distributed according to some distribution <math> p(V)</math>. Usually, the hopping amplitude <math> t_{xy}=t</math> is chosen to be uniform. | |||
To see whether localization occurs, consider a quantum particle initialised on the site <math>x_0 </math> at <math> t=0 </math>. The <ins>return probability amplitude </ins>, i.e. the probability amplitude to find the particle on the same site at later time, is | |||
<center> | |||
<math> | |||
\mathcal{A}_{x_0}(t)= \theta(t) \langle x_0| e^{-i t H} | x_0 \rangle. | |||
</math> | |||
</center> | |||
When the system is not localized, the wave function of the particle spreads in time, and the return probability decays. | |||
</li> | |||
<br> | |||
<li> <strong> Green functions and self-energies. </strong> We introduce two functions on the complex plane: the <ins>Green functions</ins> <math> G_{xy}(z) </math> and the <ins>local self-energies</ins> <math> \sigma_x(z)</math>, where <math>z=E+ i \eta, \quad \quad \eta>0</math> belongs to the upper half of the complex plane. The functions are defined by | |||
<center> | |||
<math> | |||
G_{xy}(z)= \langle x| \frac{1}{z-H}| y \rangle , \quad \quad G_{x x}(z)= \langle x| \frac{1}{z-H}| x\rangle = \frac{1}{z- V_x-\sigma_x(z)}. | |||
</math> | |||
</center> | |||
They are random functions, because the Hamiltonian contains randomness. The Green functions and the self-energies encode properties on the spectrum of the Hamiltonian; for example, the <ins> local density of eigenvalues </ins> <math>\rho_{x, N}(E)</math> for an Hamiltonian on a lattice of size <math> N </math> is indeed given by | |||
<center> <math> | |||
\rho_{x,N}(E)=-\frac{1}{\pi}\lim_{\eta \to 0} \Im G_{xx}(E+ i \eta) = \sum_{\alpha=1}^N |\langle E_\alpha| x\rangle|^2 \delta(E-E_\alpha), | |||
</math> | |||
</center> | |||
where <math> E_\alpha </math> are the eigenvalues of the full Hamiltonian <math> H </math> and <math> |E_\alpha \rangle </math> the corresponding eigenstates. When the kinetic term <math>T </math> in the Hamiltonian vanishes, the local self-energies vanish. they encode how much the energy levels <math> V_x </math> (that are the eigenvalues when <math> V=0</math>) are shifted by the presence of the kinetic term <math>T </math>. | |||
</li> | |||
<br> | |||
**** | |||
<li> <strong> Green functions and self-energies. </strong> Given a lattice with <math> N </math> sites <math>a </math>, we call <math> |a \rangle </math> the wave function completely localised in site <math> a </math>. The Anderson model has Hamiltonian | <li> <strong> Green functions and self-energies. </strong> Given a lattice with <math> N </math> sites <math>a </math>, we call <math> |a \rangle </math> the wave function completely localised in site <math> a </math>. The Anderson model has Hamiltonian | ||
<center> | <center> | ||
Revision as of 18:14, 16 March 2025
Goal: the goal of this set of problems is to derive a criterion for localization on a peculiar lattice, the Bethe lattice.
Techniques: green functions, recursion relations, cavity method.
A criterion for localization: vanishing decay rate
- Anderson model and return probability. Consider a lattice with sites . We call the wave function completely localised in site . The Anderson model has Hamiltonian:
where the local fields are random variables, independent and distributed according to some distribution . Usually, the hopping amplitude is chosen to be uniform.
To see whether localization occurs, consider a quantum particle initialised on the site at . The return probability amplitude , i.e. the probability amplitude to find the particle on the same site at later time, is
When the system is not localized, the wave function of the particle spreads in time, and the return probability decays.
- Green functions and self-energies. We introduce two functions on the complex plane: the Green functions and the local self-energies , where belongs to the upper half of the complex plane. The functions are defined by
They are random functions, because the Hamiltonian contains randomness. The Green functions and the self-energies encode properties on the spectrum of the Hamiltonian; for example, the local density of eigenvalues for an Hamiltonian on a lattice of size is indeed given by
where are the eigenvalues of the full Hamiltonian and the corresponding eigenstates. When the kinetic term in the Hamiltonian vanishes, the local self-energies vanish. they encode how much the energy levels (that are the eigenvalues when ) are shifted by the presence of the kinetic term .
- Green functions and self-energies. Given a lattice with sites , we call the wave function completely localised in site . The Anderson model has Hamiltonian
where the local fields are random variables, independent and distributed according to some distribution . We introduce the Green functions and the local self-energies these are functions of a complex variable belonging to the upper half of the complex plane,
and are defined by
When the kinetic term in the Hamiltonian vanishes, the local self-energies vanish. They are random functions, because the Hamiltonian contains randomness.
- Self-energies and return probabilities. The local self-energies encode some information on the system’s dynamics, and thus on whether localization occurs. Consider a quantum particle initialised on the site at . The return probability amplitude , i.e. the probability amplitude to find the particle on the same site at later time, is
If the self-energy has a non-zero imaginary part (when ):
then one can easily show (Residue theorem) that the return probability amplitude decays exponentially
Therefore, the system is not localized, since the probability to find it, at , in the same configuration where it was at decays very fast.
- A criterion for localization. Motivated by the reasoning above, one can claim that localization occurs whenever the imaginary part of goes to zero when . Given the randomness, this criterion should however be formulated probabilistically, as
- Green functions identities. Consider an Hamiltonian split into two parts, . Show that the following general relation for the Green functions holds:
- Cavity equations. We now apply this to a specific example: we consider a Bethe lattice, and choose one site 0 as the root. We then choose to be the kinetic terms connecting the root to its neighbours ,
For all the with we introduce the notation
where is the self energy associated to . Show that, due to the geometry of the lattice, with this choice of the Hamiltonian is decoupled and is the local Green function that one would have obtained removing the root 0 from the lattice, i.e., creating a “cavity” (hence the suffix). Moreover, using the relation above show that
Iterating this argument, show that if denotes the collection of “descendants" of , i.e. sites that are nearest neighbours of except the root, then
- Equations for the distribution. Justify why the cavity functions appearing in the denominators in the last equations above are independent and identically distributed random variables, and therefore the cavity equations can be interpreted as self-consistent equations for the distribution of the cavity functions.
- The “localized" solution. We set and . Show that the cavity equation for the self-energies is equivalent to the following pair of coupled equations:
Justify why the solution corresponding to localization, , is always a solution when ; moreover, in the localized phase when is finite but small one has . How can one argue that this solution has to be discarded, i.e. that delocalisation occurs?
- The Anderson model was formulated by P. W. Anderson in 1958, in the paper Absence of diffusion in certain random lattices , Phys. Rev. 109, 1492.
Problems
Problem 8: the Bethe lattice, recursion relations and cavity
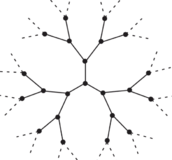
The Bethe lattice is a lattice with a regular tree structure: each node has a fixed number of neighbours , where is the branching number, and there are no loops (see sketch). In these problems we consider the Anderson model on such lattice.
Check out: key concepts of this TD
Green functions, self-energies, return probability amplitude, decay rates, trees and cavity method, the criterion for localization.