LBan-II

Introduction: Interfaces and Directed Polymers

The physical properties of many materials are governed by manifolds embedded in them. Examples include: dislocations in crystals, domain walls in ferromagnets or vortex lines in superconductors. We fix the following notation: - $D$: spatial dimension of the embedding medium – $d$: internal dimension of the manifold – $N$: dimension of the displacement (or height) field

These satisfy the relation:

$D=d+N$

We focus on two important cases:

Directed Polymers (d = 1)

The configuration is described by a vector function: $\overrightarrow{x}(t)$, where $t$ is the internal coordinate. The polymer lives in $D=1+N$ dimensions.

Examples: vortex lines, DNA strands, fronts.

Although polymers may form loops, we restrict to directed polymers, i.e., configurations without overhangs or backward turns.

Interfaces (N = 1)

The interface is described by a scalar height field: $h(\overrightarrow{r},t)$, where $\overrightarrow{r}\in {\mathbb{ℝ}}^d$ is the internal coordinate and $t$ represents time.

Examples: domain walls and propagating fronts

Again we neglect overhangs or pinch-off: $h(\overrightarrow{r},t)$ is single-valued

Note that using our notation the 1D front is both an interface and a directed polymer

Directed Polymers on a lattice

Sketch of the discrete Directed Polymer model. At each time the polymer grows either one step left either one step right. A random energy $V(\tau ,x)$ is associated at each node and the total energy is simply $E[x(\tau )]=\sum _{\tau =0}^{t}V(\tau ,x)$.

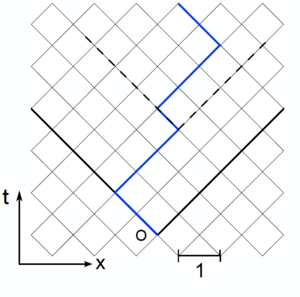
We introduce a lattice model for the directed polymer (see figure). In a companion notebook we provide the implementation of the powerful Dijkstra algorithm. Dijkstra allows to identify the minimal energy among the exponential number of configurations $x(\tau )$

$E_{\min }=\underset{x(\tau )}{\min }E[x(\tau )].$

We are also interested in the ground state configuration $x_{\min }(\tau )$. For both quantities we expect scale invariance with two exponents $\theta ,\zeta$ for the energy and for the roughness

$E_{\min }=c_{\mathrm{\infty }}t+{\kappa }_1{t}^{\theta }\chi ,x_{\min }(t/2))\sim {\kappa }_2{t}^{\zeta }\tilde{\chi }$

Universal exponents: Both $\theta ,\zeta$ are Independent of the lattice, the disorder distribution, the elastic constants, or the boudanry conditions.

Non-universal constants: $c_{\mathrm{\infty }},{\kappa }_1,{\kappa }_2$ are of order 1 and depend on the lattice, the disorder distribution, the elastic constants... However $c_{\mathrm{\infty }}$ is independent on the boudanry conditions!

Universal distributions: $\chi ,\tilde{\chi }$ are instead universal, but depends on the boundary condtions. Starting from 2000 a magic connection has been revealed between this model and the smallest eigenvalues of random matrices. In particular I discuss two different boundary conditions:

• Droplet: $x(\tau =0)=x(\tau =t)=0$. In this case, up to rescaling, $\chi$ is distributed as the smallest eigenvalue of a GUE random matrix (Tracy Widom distribution $F_2(\chi )$)

• Flat: $x(\tau =0)=0$ while the other end $x(\tau =t)$ is free. In this case, up to rescaling, $\chi$ is distributed as the smallest eigenvalue of a GOE random matrix (Tracy Widom distribution $F_1(\chi )$)

Entropy and scaling relation

It is useful to compute the entropy

$\text{Entropy}=\ln (\genfrac{}{}{0ex}{}{t}{\frac{t-x}{2}})\approx t\ln 2-\frac{x^2}{t}+O(x^4)$

From which one could guess from dimensional analysis

$\theta =2\zeta -1$

This relation is actually exact also for the continuum model.

Directed polymers in the continuum

We now reanalyze the previous problem in the presence of quenched disorder. Instead of discussing the case of interfaces, we will focus on directed polymers. Let us consider polymers $x(\tau )$ of length $t$. The energy associated with a given polymer configuration can be written as

$E[x(\tau )]=\underset{0}{\overset{t}{\int }}d\tau [\frac{1}{2}{\left(\frac{dx}{d\tau }\right)}^2+V(x(\tau ),\tau )]$

The first term describes the elastic energy of the polymer, while the second one is the disordered potential, which we assume to be

$\overline{V(x,\tau )}=0,\overline{V(x,\tau )V(x^{\prime },{\tau }^{\prime })}=D\delta (x-x^{\prime })\delta (\tau -{\tau }^{\prime }).$

where 'D' is the disorder strength.

Polymer partition function and propagator of a quantum particle

Let us consider polymers starting in $0$, ending in $x$ and at thermal equilibrium at temperature $T$. The partition function of the model writes as

$Z(x,t)=\underset{x(0)=0}{\overset{x(t)=x}{\int }}{𝒟}x(\tau )\exp [-\frac{1}{T}\underset{0}{\overset{t}{\int }}d\tau \frac{1}{2}({\partial }_{\tau }x{)}^2+V(x(\tau ),\tau )]$

Here, the partition function is written as a sum over all possible paths, corresponding to all possible polymer configurations that start at $0$ and end at $x$, weighted by the appropriate Boltzmann factor.

Let's perform the following change of variables: $\tau =i{t}^{\prime }$. We also identifies $T$ with $\hslash$ and $\tilde{t}=-it$ as the time.

$Z(x,\tilde{t})=\underset{x(0)=0}{\overset{x(\tilde{t})=x}{\int }}{𝒟}x(t^{\prime })\exp [\frac{i}{\hslash }\underset{0}{\overset{\tilde{t}}{\int }}d{t}^{\prime }\frac{1}{2}({\partial }_{t^{\prime }}x{)}^2-V(x(t^{\prime }),t^{\prime })]$

Note that $S[x]=\underset{0}{\overset{\tilde{t}}{\int }}d{t}^{\prime }\frac{1}{2}({\partial }_{t^{\prime }}x{)}^2-V(x(t^{\prime }),t^{\prime })$ is the classical action of a particle with kinetic energy $\frac{1}{2}({\partial }_{\tau }x{)}^2$ and time dependent potential $V(x(\tau ),\tau )$, evolving from time zero to time $\tilde{t}$. From the Feymann path integral formulation, $Z[x,\tilde{t}]$ is the propagator of the quantum particle.

Feynman-Kac formula

Let's derive the Feyman Kac formula for $Z(x,t)$ in the general case:

• First, focus on free paths and introduce the following probability

$P[A,x,t]=\underset{x(0)=0}{\overset{x(t)=x}{\int }}{𝒟}x(\tau )\exp [-\frac{1}{T}\underset{0}{\overset{t}{\int }}d\tau \frac{1}{2}({\partial }_{\tau }x{)}^2]\delta (\underset{0}{\overset{t}{\int }}d\tau V(x(\tau ),\tau )-A)$

• Second, the moments generating function

$Z_p(x,t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}dA{e}^{-pA}P[A,x,t]=\underset{x(0)=0}{\overset{x(t)=x}{\int }}{𝒟}x(\tau )e^{-\frac{1}{T}\underset{0}{\overset{t}{\int }}d\tau \frac{1}{2}({\partial }_{\tau }x{)}^2-p\underset{0}{\overset{t}{\int }}d\tau V(x(\tau ),\tau )}$

• Third, consider free paths evolving up to $t+dt$ and reaching $x$ :

$Z_p(x,t+dt)=⟨e^{-p\underset{0}{\overset{t+dt}{\int }}d\tau V(x(\tau ),\tau )}⟩=⟨e^{-p\underset{0}{\overset{t}{\int }}d\tau V(x(\tau ),\tau )}⟩e^{-pV(x,t)dt}=[1-pV(x,t)dt+\dots ]{⟨Z_p(x-\mathrm{\Delta }x,t)⟩}_{\mathrm{\Delta }x}$

Here $⟨\dots ⟩$ is the average over all free paths, while $⟨\dots {⟩}_{\mathrm{\Delta }x}$ is the average over the last jump, namely $⟨\mathrm{\Delta }x⟩=0$ and $⟨\mathrm{\Delta }{x}^2⟩=Tdt$.

• At the lowest order we have

$Z_p(x,t+dt)=Z_p(x,t)+dt[\frac{T}{2}\underset{x}{\overset{2}{\partial }}{Z}_p-pV(x,t)Z_p]+O(d{t}^2)$

Replacing $p=1/T$ we obtain the partition function is the solution of the Schrodinger-like equation:

${\partial }_{t}Z(x,t)=-\hat{H}Z=-[-\frac{T}{2}\frac{d^2}{d{x}^2}+\frac{V(x,\tau )}{T}]Z(x,t)$

$Z[x,t=0]=\delta (x)$

Remarks

Remark 1:

This equation is a diffusive equation with multiplicative noise $V(x,\tau )/T$ . Edwards Wilkinson is instead a diffusive equation with additive noise.

Remark 2: This hamiltonian is time dependent because of the multiplicative noise $V(x,\tau )/T$. For a time independent hamiltonian, we can use the spectrum of the operator. In general we will have to parts:

• A discrete set of eigenvalues $E_n$ with the eigenstates ${\psi }_n(x)$
• A continuum part where the states ${\psi }_E(x)$ have energy $E$. We define the density of states $\rho (E)$, such that the number of states with energy in ($E,E+dE$) is $\rho (E)dE$.

In this case $Z[x,t]$ can be written has the sum of two contributions:

$Z[x,t]={\left(e^{-\hat{H}t}\right)}_{0\to x}=\sum _n{\psi }_n(0){\psi }_n^{*}(x)e^{-E_{n}t}+\underset{0}{\overset{\mathrm{\infty }}{\int }}dE\rho (E){\psi }_E(0){\psi }_E^{*}(x)e^{-Et}.$

In absence of disorder, one can find the propagator of the free particle, that, in the original variables, writes:

$Z_{\text{free}}(x,t)=\frac{e^{-x^2/(2Tt)}}{\sqrt{2\pi Tt}}$