L-2

Goal: The physical properties of many materials are controlled by the interfaces embedded in it. This is the case of the dislocations in a crystal, the domain walls in a ferromagnet or the vortices in a supercoductors. In the next lecture we will discuss how impurities affect the behviour of these interfaces. Today we focus on thermal fluctuations and introduce two important equations for the interface dynamics: the Edwards Wilkinson (EW) and the Kardar Parisi Zhang (KPZ) equations.

Edwards Wilkinson: an interface at equilibrium:

Consider domain wall $h(r,t)$ fluctuating at equilibrium at the temparature $T$. Here $t$ is time, $r$ defines the d-dimensional coordinate of the interface and $h$ is the scalar height field. Hence, the domain wall separating two phases in a film has $d=1,r\in {\cal {R}}$, in a solid instead $d=2,r\in {\cal {{R}^{2}}}$.

Two assumptions are done:

• Overhangs, pinch-off are neglected, so that $h(r,t)$ is a scalar univalued function.
• The dynamics is overdamped, so that we can neglect the inertial term.

Derivation

The Langevin equation of motion is

$\partial _{t}h(r,t)=-\mu {\frac {\delta E_{pot}}{\delta h(r,t)}}+\eta (r,t)$

The first term $-\delta E_{pot}/\delta h(r,t)$ is the elastic force trying to smooth the interface, the mobility $\mu$ is inversily proportional to the viscosity. The second term is the Langevin Gaussian noise defined by the correlations

$\langle \eta (r,t)\rangle =0,\;\langle \eta (r',t')\eta (r,t)\rangle =2D\delta ^{d}(r-r')\delta (t-t')$

The symbol $\langle \ldots \rangle$ indicates the average over the thermal noise. The diffusion constant is fixed by the Eistein relation (fluctuation-dissipation theorem):

$D=\mu K_{B}T$

We set $\mu K_{B}=1$

The potential energy of surface tension can be expanded at the lowest order in the gradient:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{pot} = \nu \int d^d r\sqrt{1 +(\nabla h)^2} \sim \text{const.} + \frac{\nu}{2} \int d^d r (\nabla h)^2 }

Hence, we have the Edwards Wilkinson equation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial_t h(r,t)= \nu \nabla^2 h(r,t) + \eta(r,t) }

Scaling Invariance

The equation enjoys of a continuous symmetry because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(r,t) } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(r,t)+c } cannot be distinguished. This is a condition of scale invariance:

$h(br,b^{z}t){\overset {inlaw}{\sim }}b^{\alpha }h(r,t)$

Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z, \alpha } are the dynamic and the roughness exponent respectively. From dimensional analysis

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b^{\alpha-z} \partial_t h(r,t)= b^{\alpha-2} \nabla^2 h(r,t) +b^{-d/2-z/2} \eta(r,t) }

From which you get $z=2$ in any dimension and a rough interface below Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d=2 } with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha =(2-d)/2 } .

Exercise L2-A: Solve Edwards-Wilkinson

For simplicity, consider a 1-dimensional line of size L with periodic boundary conditions. It is useful to introduce the Fourier modes:

${\hat {h}}_{q}(t)={\frac {1}{L}}\int _{0}^{L}e^{iqr}h(r,t),\quad h(r,t)=\sum _{q}e^{-iqr}{\hat {h}}_{q}(t)$

Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=2 \pi n/L, n=\ldots ,-1,0,1,\ldots} and recall Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^L d r e^{iqr}= L \delta_{q,0} } .

• Show that the EW equation writes

$\partial _{t}{\hat {h}}_{q}(t)=-\nu q^{2}{\hat {h}}_{q}(t)+\eta _{q}(t),\quad {\text{with}}\;\langle \eta _{q_{1}}(t')\eta _{q_{2}}(t)\rangle ={\frac {T}{L}}\delta _{q_{1},-q_{2}}\delta (t-t')$

The solution of this first order linear equation writes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat h_q(t)= \hat h_q(0) e^{-\nu q^2 t} +\int_0^t d s e^{- \nu q^2 (t-s)} \eta_q(s) }

Assume that the interface is initialy flat, namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat h_q(0) =0 } .

• Compute the width $\langle h(x,t)^{2}\rangle =\sum _{q}\langle h_{q}(t)h_{-q}(t)\rangle$. Comment about the roughness and the short times growth.

KPZ equation and interface growth

Consider a domain wall in presence of a positive magnetic field. At variance with the previous case the ferromagnetic domain aligned with the field will expand while the other will shrink. The motion of the interface describes now the growth of the stable domain, an out-of-equilibrium process.

Derivation

The growth is normal (orthogonal) to the interface.

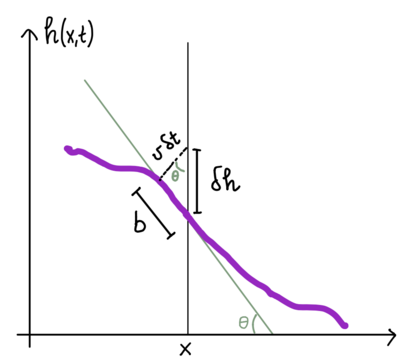
To derive the correct equation of a growing interface the key point is to realize that the growth occurs locally along the normal to the interface (see figure).

Let us call Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} the velocity of the interface. Consider a point of the interface Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(r,t)} , its tangent is $\partial _{r}h(r,t)=-\tan(\theta )$. To evaluate the increment Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta h(r,t)} use the Pitagora theorem:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta h(r,t)= \sqrt{(v dt)^2 + (v dt \tan(\theta))^2 } \sim v dt + \frac{v dt}{2} (\tan(\theta))^2 \sim v dt + \frac{v dt}{2} (\partial_r h(r,t))^2 }

Hence, in generic dimension, the KPZ equation is

$\partial _{t}h(r,t)=\nu \nabla ^{2}h(r,t)+{\frac {\lambda }{2}}(\nabla h)^{2}+\eta (r,t)$

Scaling Invariance

The symmetry Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h +c } still holds so that scale invariance is still expected. However the non-linearity originate an anomalous dimension and $z,\alpha$ cannot be determined by simple dimensional analysis.

An important symmetry

Let us remark that if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(r,t) } is a solution of KPZ,also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde h(r,t)= h(r + \lambda v_0 t,t) +v_0 r +(v_0^2 \lambda /2) t } is a solution of KPZ, provided the change of variables ${\tilde {r}}=r+\lambda v_{0}t$ . You can check it, and you will obtain an equation with the statistically equivalent noise Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta(\tilde{r} - \lambda v_0 t,t)} . The symmetry relies on two properties:

• The noise Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta(r,t) } is delta correlated in time
• Only sticked together the two terms $\partial _{t}h(r,t)$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\lambda}{2} (\partial_r h(r,t))^2} enjoy the symmetry. Hence, under the rescaling

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b^{\alpha-z} \left( \partial_t h(r,t)- b^{ \alpha+z-2 } \frac{\lambda}{2} (\partial_r h(r,t))^2\right)}

the second term should be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b } -independent. This provides a new and exact scaling relation

$z+\alpha =2$

The d=1 case

In the one dimensional case the KPZ equation writes Hence, in generic dimension, the KPZ equation is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial_t h(r,t)= \nu \partial_r^2 h(r,t)+ \frac{\lambda}{2} (\partial_r h)^2 + \eta(r,t) }

The corresponding Fokker Planck equation for the probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\cal} P[h,t] } can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial_t {\cal P}= - \int d r \frac{\delta}{\delta h_r} \left\{\left[\nu \partial_r^2 h +\frac{\lambda}{2} (\partial_r h)^2 \right] {\cal P} \right\} +T \int d r \frac{\delta^2 {\cal P}}{\delta h_r^2} }

The probability

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\cal P}_{st} [h] \propto \exp\left\{- \frac{1}{T}\int d r \; \frac{\nu}{2} (\partial_r h)^2 \right\} }

is a stationary solution (namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial_t{\cal P}_{st} [h]=0} )for EW as you can check

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \frac{\delta {\cal P}_{st} }{\delta h_r} - \nu \partial_r^2 h {\cal P}_{st} =0 }

It is also a solution (only for $d=1$)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d r \frac{\delta}{\delta h_r} \left[\frac{\lambda}{2} (\partial_r h)^2 {\cal P}_{st} \right] =0 }

even if the last equality has some issues of disretization. As a conclusion in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d=1} we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=1/2} as for EW, but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=3/2} .