T-I

Goal: derive the equilibrium phase diagram of the simplest spin-glass model, the Random Energy Model (REM). The REM is defined assigning to each configuration $\alpha$ of the system a random energy $E_{\alpha }$. The random energies are independent, taken from a Gaussian distribution $p(E)=(2\pi N)^{-1/2}e^{-{\frac {E^{2}}{2N}}}$.

Key concepts: average value vs typical value, large deviations, rare events, saddle point approximation, self-averaging quantities, freezing transition, .

A dictionary for large $N$ disordered systems

• Exponentially scaling variables. We will consider random variables $X_{N}$ which depend on a parameter $N\gg 1$ (the number of degrees of freedom: for a system of size $L$ in dimension $d$, $N=L^{d}$) and which have the scaling $X_{N}\sim O(e^{N})$; the scaling means that the rescaled variable $Y_{N}=N^{-1}\log |X_{N}|$ has a well defined distribution that remains of $O(1)$ when $N\to \infty$. The standard example we have in mind are the partition functions of disordered systems with $N$ degrees of freedom, $Z\sim e^{-\beta Nf}$: here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N \to Z } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N \to -\beta f } , where $f$ is the free energy density. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_N(x), P_N(y) } be the distributions of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } and $Y_{N}$.


• Self-averaging. A random variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N } is self-averaging when, in the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \to \infty } , its distribution concentrates around the average, collapsing to a delta function:

  $\lim _{N\to \infty }Y_{N}=\lim _{N\to \infty }{\overline {Y_{N}}}.$

  This happens when its fluctuations are small compared to the average, meaning that

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{N \to \infty} \frac{\overline{Y_N^2}}{\overline{Y_N}^2}=1. }

  When the random variable is not self-averaging, it remains distributed in the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \to \infty } . The property of being self-averaging holds for the free energy of the systems we will consider. It is a very important property: the free energy (and therefore all the thermodynamics observables, that can be obtained taking derivatives of the free energy) does not fluctuate from sample to sample when $N$ is large. Notice that while quantities like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N } (like the free energy density) are self-averaging, quantities scaling exponentially like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } (like the partition function) are not necessarily so, see below.



• Average and typical values. For self-averaging quantities, the asymptotic value is their average value, which in general is also their typical value. In general, quantities like $Y_{N}$ have a distribution that for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } takes the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_N(y) \sim e^{-N^\omega g(y)+ \text{subleading}} } where $g(y)$ is some positive function and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega>0 } . This is called a large deviation form for the probability distribution, with speed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^\omega } . This distribution is of $O(1)$ for the value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}} } such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(y_{\text{ty}})=0 } : this value is the typical value of $Y_{N}$; all the other values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } are associated to a probability that is exponentially small in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^\omega} : they are exponentially rare.
  Averages over distributions having a large deviation form can usually be computed with the saddle point approximation for large $N$. Let’s fix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega=1 } . If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(Y_N) } is a function of $Y_{N}$ which scales slower than exponential of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } , then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{f(Y_N)} =\int dy P_N(y) f(y)= \int dy\, e^{-N g(y)+o(N)} f(y) \sim f(y_{\text{ty}}) }

  because the integral is dominated by the region where $g(y)=0$, since all the other contributions are exponentially suppressed. This also implies (choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y)=y } )

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{N \to \infty} Y_N =\lim_{N \to \infty} \overline{Y_N}= y_{\text{ty}} }



• Quenched averages. Let us go back to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } : how to get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}} } from it? We have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}} =\lim_{N \to \infty} Y_N= \lim_{N \to \infty} \frac{\overline{\log |X_N|}}{N}= \lim_{N \to \infty} \frac{\overline{\log x_{\text{ty}}}}{N} }

  since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\log |X_N|}=\int dx P_N(x) \log |x| = N \int dy P_N(y) \, y= N \int dy\, e^{-N g(y)+o(N)} \, y \sim N y_{\text{ty}}} , and we have identified Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}}= \lim_{N \to \infty} N^{-1} \log x_{\text{ty}} } .

  In the language of disordered systems, computing the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } through the average of its logarithm corresponds to performing a quenched average: from this average, one extracts the correct asymptotic value of the self-averaging quantity $Y_{N}$.


• Annealed averages. The quenched average does not necessarily coincide with the annealed average, defined as:

  $y_{\text{a}}=\lim _{N\to \infty }{\frac {\log {\overline {|X_{N}|}}}{N}}.$

  In fact, it always holds Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\log |X_N|} \leq \log |\overline{X_N}|} because of the concavity of the logarithm. One case in which the inequality is strict, and thus quenched and annealed averages are not the same, is when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } is not self-averaging, and its average value is typically much larger than the typical value at large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } (because the average is dominated by rare events). In this case, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{a}} \neq y_{\text{ty}}} , and to get the correct limit of the self-averaging quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N } one has to perform the quenched average.

Notice that not vice-versa: you can have quenched equals annealed without X being self averaging.

Problem 1.1: the energy landscape of the REM

Entropy of the Random Energy Model

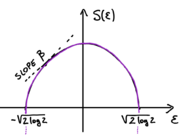
In this problem we study the random variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}(E)dE } , that is the number of configurations having energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\alpha \in [E, E+dE] } . We show that for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } it scales as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}(E) = e^{N S\left( E/N\right) + o(N)}} . We show that the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\epsilon) } , the quenched entropy of the model (see sketch), is given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\epsilon)=\begin{cases} \log 2- \epsilon^2 \quad &\text{ if } |\epsilon| \leq \sqrt{\log 2} \\ 0 \quad &\text{ if } |\epsilon| >\sqrt{\log 2} \end{cases} }

The point where the entropy vanishes, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=- \sqrt{\log 2} } , is the energy density of the ground state. The entropy is maximal at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=0 } : the highest number of configurations have vanishing energy density.

1. Averages: the annealed entropy. We begin by computing the annealed entropy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\text{a}} } , which is defined by the average Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\mathcal{N}(E)}= \text{exp}\left(N S_{\text{a}}\left( E/N \right)+ o(N)\right) } . Compute this function using the representation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}(E)dE= \sum_{\alpha=1}^{2^N} \chi_\alpha(E) dE \;} [with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_\alpha(E)=1} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\alpha \in [E, E+dE]} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_\alpha(E)=0} otherwise]. When does Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\text{a}} } coincide with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S } ?

2. Self-averaging. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\epsilon| \leq \sqrt{\log 2} } the quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } is self-averaging: its distribution concentrates around the average value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\mathcal{N}} } when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \to \infty } . Show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2= \overline{\mathcal{N}^2}- \overline{\mathcal{N}}^2 \sim \overline{\mathcal{N}}} ; by the central limit theorem, show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } is self-averaging when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\epsilon|< \sqrt{\log 2} } . This is no longer true in the region where the annealed entropy is negative: why does one expect fluctuations to be relevant in this region?

3. Rare events vs typical values. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\epsilon| > \sqrt{\log 2} } the annealed entropy is negative: the average number of configurations with those energy densities is exponentially small in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } . This implies that the probability to get configurations with those energy is exponentially small in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } : these configurations are rare. Do you have an idea of how to show this, using the expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\mathcal{N}}} ? What is the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } in this region? Justify why the point where the entropy vanishes coincides with the ground state energy of the model.

Problem 1.2: the free energy and the freezing transition

We now compute the equilibrium phase diagram of the model, and in particular the quenched free energy density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } which controls the scaling of the typical value of the partition function, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \sim e^{-N \beta \, f +o(N) } } . We show that the free energy equals to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \begin{cases} &- \left( T \log 2 + \frac{1}{4 T}\right) \quad \text{if} \quad T \geq T_c\\ & - \sqrt{\log 2} \quad \text{if} \quad T <T_c \end{cases} \quad \quad T_c= \frac{1}{2 \sqrt{\log 2}}. }

At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c } a transition occurs, often called freezing transition: in the whole low-temperature phase, the free-energy is “frozen” at the value that it has at the critical temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T= T_c } .

1. The thermodynamical transition and the freezing. The partition function the REM reads Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = \sum_{\alpha=1}^{2^N} e^{-\beta E_\alpha}= \int dE \, \mathcal{N}(E) e^{-\beta E}. } Using the behaviour of the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } determined in Problem 1.1, derive the free energy of the model (hint: perform a saddle point calculation). What is the order of this thermodynamic transition?

2. Entropy. What happens to the entropy of the model when the critical temperature is reached, and in the low temperature phase? What does this imply for the partition function $Z$?

3. Fluctuations, and back to average vs typical. Similarly to what we did for the entropy, one can define an annealed free energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\text{a}} } from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{Z}=e^{- N \beta f_{\text{a}} + o(N)} } : show that in the whole low-temperature phase this is smaller than the quenched free energy obtained above. Putting all the results together, justify why the average of the partition function in the low-T phase is "dominated by rare events".

Comment: the low-T phase of the REM is a frozen phase, characterized by the fact that the free energy is temperature independent, and that the typical value of the partition function is very different from the average value. In fact, the low-T phase is also a glass phase : it is a phase where a peculiar symmetry, the so called replica symmetry, is broken. We go back to this concepts in the next sets of problems.