T-I

Goal: derive the equilibrium phase diagram of the simplest spin-glass model, the Random Energy Model (REM).
Techniques: saddle point approximation, Legendre transform, probability theory.

A dictionary for large-N disordered systems

• Exponentially scaling variables. We will consider positive random variables $X_{N}$ which depend on a parameter $N\gg 1$ (the number of degrees of freedom: for a system of size $L$ in dimension $d$, $N=L^{d}$) and which have the scaling $X_{N}\sim e^{NY_{N}}$: this means that the rescaled variable $Y_{N}=N^{-1}\log X_{N}$ has a well defined distribution that remains of $O(1)$ when $N\to \infty$. The standard example we have in mind are the partition functions of disordered systems with $N$ degrees of freedom, $Z_{N}\sim e^{-\beta Nf_{N}}$: here $X_{N}\to Z_{N}$ and $Y_{N}\to -\beta f_{N}$, where $f_{N}$ is the free energy density. Let $P_{X_{N}}(x),P_{Y_{N}}(y)$ be the distributions of $X_{N}$ and $Y_{N}$.


• Self-averaging. A random variable $Y_{N}$ is self-averaging when, in the limit $N\to \infty$, its distribution concentrates around the average, collapsing to a delta function:

  $\lim _{N\to \infty }Y_{N}=\lim _{N\to \infty }{\overline {Y_{N}}}\equiv {\overline {Y_{\infty }}}.$

  This happens when its fluctuations are small compared to the average, meaning that

  $\lim _{N\to \infty }{\frac {\overline {Y_{N}^{2}}}{{\overline {Y_{N}}}^{2}}}=1.$

  When the random variable is not self-averaging, it remains distributed in the limit $N\to \infty$. When it is self-averaging, sample-to-sample fluctuations are suppressed when $N$ is large. This property holds for the free energy of all the disordered systems we will consider. This is very important property: it implies that the free energy (and therefore all the thermodynamics observables, that can be obtained taking derivatives of the free energy) does not fluctuate from sample to sample when $N$ is large, and so the physics of the system does not depend on the particular sample. Notice that while quantities like $Y_{N}$ (like the free energy density) are self-averaging, quantities scaling exponentially like $X_{N}$ (like the partition function) are not necessarily so, see below.



• Average and typical. The typical value of a random variable is the value at which its distribution peaks. When does this coincide with the average value? We discuss an example.
  Often, quantities like $Y_{N}$ have a distribution that for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } takes the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{Y_N}(y) \sim e^{-N^\omega g(y)+ \text{subleading}} } where $g(y)$ is some positive function and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega>0 } . This is called a large deviation form for the probability distribution, with speed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^\omega } . This distribution is of $O(1)$ for the value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}} } such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(y_{\text{ty}})=0 =g'(y_{\text{ty}})} : this value is the typical value of $Y_{N}$; all the other values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } are associated to a probability that is exponentially small in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^\omega} : they are exponentially rare. Averages over distributions having a large deviation form can usually be computed with the saddle point approximation for large $N$. Let’s fix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega=1 } . If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(Y_N) } is a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N } which scales slower than exponential of $N$ then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{F(Y_N)} =\int dy\, P_{Y_N}(y)\, F(y)= \int dy\, e^{-N g(y)+o(N)} F(y) \sim F(y_{\text{ty}}) }

  because the integral is dominated by the region where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(y)=0 } , since all the other contributions are exponentially suppressed. This also implies (choose $F(y)=y$)

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{N \to \infty} Y_N = \overline{Y_\infty}= y_{\text{ty}} }



• Quenched averages. Let us go back to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } : how to get $y_{\text{ty}}$ from it? When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N } is self-averaging, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}} =\lim_{N \to \infty} \overline{Y_N}= \lim_{N \to \infty} \frac{\overline{\log X_N}}{N} \equiv \lim_{N \to \infty} \frac{{\log x_{\text{ty}}}}{N} }

  where in the last line we have used that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{ty}}= \lim_{N \to \infty} N^{-1} \log x_{\text{ty}} } .

  In the language of disordered systems, computing the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } through the average of its logarithm corresponds to performing a quenched average: from this average, one extracts the correct asymptotic value of the self-averaging quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_N } .


• Annealed averages. The quenched average does not necessarily coincide with the annealed average, defined as:

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{\text{a}} = \lim_{N \to \infty} \frac{\log \overline{X_N}}{N}. }

  In fact, it always holds Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\log X_N} \leq \log \overline{X_N}} because of the concavity of the logarithm. One case in which the inequality is strict, and thus quenched and annealed averages are not the same, is when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_N } is not self-averaging, and its average value is exponentially larger than the typical value (because the average is dominated by rare events). In this case, $y_{\text{a}}\neq y_{\text{ty}}$, and to get the correct limit of the self-averaging quantity $Y_{N}$ one has to perform the quenched average.^[*] This is what happens in the glassy phase.

[*] - Notice that the opposite is not true: one can have situations in which the partition function is not self-averaging, but still the quenched free energy coincides with the annealed one.

Problem 1.1: the energy landscape of the REM

Entropy of the Random Energy Model

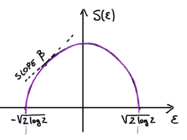
The REM has been introduced in ^[1] . In the REM the system can take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^N } configurations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec S=(S_1, \cdots, S_N)} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i = \pm 1 } . To each configuration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=1, \cdots, 2^N} is assigned a random energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\alpha} . The random energies are independent, taken from a Gaussian distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(E) =( \pi N)^{-1/2}e^{-\frac{E^2}{ N}}} . In this problem we study the random variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}(E)dE } , that is the number of configurations having energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\alpha \in [E, E+dE] } . We show that for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } it scales as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}(E) = e^{N S\left( E/N\right) + o(N)}} . We show that the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\epsilon) } , the quenched entropy of the model (see sketch), is given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\epsilon)=\begin{cases} \log 2- \epsilon^2 \quad &\text{ if } |\epsilon| \leq \sqrt{\log 2} \\ 0 \quad &\text{ if } |\epsilon| >\sqrt{\log 2} \end{cases} }

The point where the entropy vanishes, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=- \sqrt{\log 2} } , is the energy density of the ground state. The entropy is maximal at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=0 } : the highest number of configurations have vanishing energy density.

1. Averages: the annealed entropy. We begin by computing the annealed entropy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\text{a}} } , which is defined by the average Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\mathcal{N}(E)}= \text{exp}\left(N S_{\text{a}}\left( E/N \right)+ o(N)\right) } . Compute this function using the representation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}(E)dE= \sum_{\alpha=1}^{2^N} \chi_\alpha(E) dE \;} [with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_\alpha(E)=1} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\alpha \in [E, E+dE]} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_\alpha(E)=0} otherwise]. When does Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\text{a}} } coincide with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S } ?

2. Self-averaging. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\epsilon| \leq \sqrt{\log 2} } the quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } is self-averaging: its distribution concentrates around the average value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\mathcal{N}} } when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \to \infty } . Show this by showing that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2= \overline{\mathcal{N}^2}- \overline{\mathcal{N}}^2 \sim \overline{\mathcal{N}}} . This property of being self-averaging is no longer true in the region where the annealed entropy is negative: why does one expect fluctuations to be relevant in this region?

3. Rare events vs typical values. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\epsilon| > \sqrt{\log 2} } the annealed entropy is negative: the average number of configurations with those energy densities is exponentially small in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } . This implies that the probability to get configurations with those energy is exponentially small in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } : these configurations are rare. Do you have an idea of how to show this, using the expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\mathcal{N}}} ? What is the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } in this region? Justify why the point where the entropy vanishes coincides with the ground state energy of the model.

Problem 1.2: the free energy and the freezing transition

We now compute the equilibrium phase diagram of the model, and in particular the quenched free energy density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } which controls the scaling of the typical value of the partition function, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \sim e^{-N \beta \, f +o(N) } } . We show that the free energy equals to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \begin{cases} &- \left( T \log 2 + \frac{1}{4 T}\right) \quad \text{if} \quad T \geq T_c\\ & - \sqrt{\log 2} \quad \text{if} \quad T <T_c \end{cases} \quad \quad T_c= \frac{1}{2 \sqrt{\log 2}}. }

At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c } a transition occurs, often called freezing transition: in the whole low-temperature phase, the free-energy is “frozen” at the value that it has at the critical temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T= T_c } .

1. The thermodynamical transition and the freezing. The partition function the REM reads Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = \sum_{\alpha=1}^{2^N} e^{-\beta E_\alpha}= \int dE \, \mathcal{N}(E) e^{-\beta E}. } Using the behaviour of the typical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} } determined in Problem 1.1, derive the free energy of the model (hint: perform a saddle point calculation). What is the order of this thermodynamic transition?

2. Entropy. What happens to the entropy of the model when the critical temperature is reached, and in the low temperature phase? What does this imply for the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} ?

3. Fluctuations, and back to average vs typical. Similarly to what we did for the entropy, one can define an annealed free energy $f_{\text{a}}$ from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{Z}=e^{- N \beta f_{\text{a}} + o(N)} } : show that in the whole low-temperature phase this is smaller than the quenched free energy obtained above. Putting all the results together, justify why the average of the partition function in the low-T phase is "dominated by rare events".

Comment: the low-T phase of the REM is a frozen phase, characterized by the fact that the free energy is temperature independent, and that the typical value of the partition function is very different from the average value. In fact, the low-T phase is also a glass phase : it is a phase where a peculiar symmetry, the so called replica symmetry, is broken. We go back to this concepts in the next sets of problems.

Check out: key concepts

Self-averaging, average value vs typical value, large deviations, rare events, saddle point approximation, freezing transition.

To know more

• Derrida. Random-energy model: limit of a family of disordered models [1]