TBan-II

Dijkstra Algorithm and transfer matrix

Sketch of the discrete Directed Polymer model. At each time the polymer grows either one step left either one step right. A random energy $V(\tau ,x)$ is associated at each node and the total energy is simply $E[x(\tau )]=\sum _{\tau =0}^{t}V(\tau ,x)$.

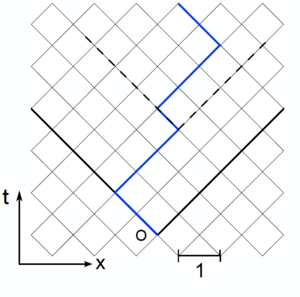
We introduce a lattice model for the directed polymer (see figure). In a companion notebook we provide the implementation of the powerful Dijkstra algorithm.

Dijkstra allows to identify the minimal energy among the exponential number of configurations $x(\tau )$

$E_{\min }=\min _{x(\tau )}E[x(\tau )].$

We are also interested in the ground state configuration $x_{\min }(\tau )$. For both quantities we expect scale invariance with two exponents $\theta ,\zeta$ for the energy and for the roughness

$E_{\min }=c_{\infty }t+b_{\infty }t^{\theta }\chi ,\quad x_{\min }(t/2))\sim a_{\infty }t^{\zeta }{\tilde {\chi }}$

Universal exponents: Both $\theta ,\zeta$ are Independent of the lattice, the disorder distribution, the elastic constants, or the boudanry conditions. Note that $\omega =\theta$, while for an interface $\omega =d\theta$.

Non-universal constants: $c_{\infty },b_{\infty },a_{\infty }$ are of order 1 and depend on the lattice, the disorder distribution, the elastic constants... However $c_{\infty }$ is independent on the boudanry conditions!

Universal distributions: $\chi ,{\tilde {\chi }}$ are instead universal, but depends on the boundary condtions. Starting from 2000 a magic connection has been revealed between this model and the smallest eigenvalues of random matrices. In particular I discuss two different boundary conditions:

• Droplet: $x(\tau =0)=x(\tau =t)=0$. In this case, up to rescaling, $\chi$ is distributed as the smallest eigenvalue of a GUE random matrix (Tracy Widom distribution $F_{2}(\chi )$)

• Flat: $x(\tau =0)=0$ while the other end $x(\tau =t)$ is free. In this case, up to rescaling, $\chi$ is distributed as the smallest eigenvalue of a GOE random matrix (Tracy Widom distribution $F_{1}(\chi )$)

Entropy and scaling relation

It is useful to compute the entropy

${\text{Entropy}}=\ln {\binom {t}{\frac {t-x}{2}}}\approx t\ln 2-{\frac {x^{2}}{t}}+O(x^{4})$

From which one could guess from dimensional analysis

$\theta =2\zeta -1$

We will see that this relation is actually exact.