Introduction à l’intégrale de chemin – Application pour la mécanique quantique, la physique statistique et l’étude des processus aléatoires
Enseignement au Master CFP, parcours de physique quantique, à l’E.N.S


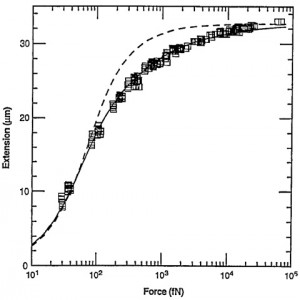
Bustamante et al, Science 265, 1599 (9 september 1994)
2005-2010 : TD (1er semestre)
2010-2012 : TD, Option de 2nd semestre
Cours :
Le cours est assuré par Alain Comtet, Professeur à l’Université Pierre et Marie Curie.
Sujets de TD :
- TD 1: Généralités.
- TD 2: Intégrale de chemin pour l’oscillateur harmonique.
- TD 3: Approximation semiclassique et effet tunnel — Application à l’étude des singularité de Lifshitz de la DoS d’hamiltonien désordonnés par la méthode des répliques.
- TD 4: Élasticité des polymères.
- TD 5: Formule de Feynman-Kac (annexe : autres propriétés des marches aléatoires et du mvt brownien).
- TD 6: Équation de Langevin et de Fokker-Planck. Distribution de temps de premier passage.
Application pour l’étude de la localisation forte undimensionnelle.
Quelques sujets d’examen :
- Examen 2007-2008 : Accrochage d’un polymère (3D)
- Examen 2008-2009 : Distribution du maximum d’un pont brownien — Enroulement et correction de localisation faible
- Examen 2009-2010 : Distribution du temps local pour processus de Wiener et accrochage d’un polymère 1D
- Examen 2011-2012 : Constante de diffusion pour une courbe brownienne unique — Particule dans un champ de gravitation — Polymère dirigé en milieu désordonné
- Examen 2012-2013 : Temps de séjour pour un pont brownien — Molécule d’ADN dans un écoulement fluide